Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 12. 2011 14:36
Integrál - substituce
Dobrý den, jako asi většina studentů jsem si začal propočítávat vzorové příklady ke zkoušce a u jednoho příkladu z Analýzy mne zarazila následující věc.
Zadání: Vypočtěte
U výsledku od přednášející je ale uvedena substituce  , která se však používá pouze pro sudé mocniny, nebo součin Sin(x)Cos(x) a ne substituce
, která se však používá pouze pro sudé mocniny, nebo součin Sin(x)Cos(x) a ne substituce 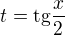 používaná pro obecné případy.
používaná pro obecné případy.
Uvedený výsledek je 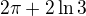
Ocenil bych kdyby mi někdo ujasnil, jestli se pletu pouze já a lze zde použít uvedenou substituci a nebo se jedná pouze o překlep přednášející.
Offline
#2 30. 12. 2011 14:45 — Editoval vanok (30. 12. 2011 14:54)
Re: Integrál - substituce
Ahoj [re]p246908|Mirianel],
Da sa vidiet ze plati: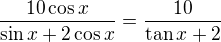
Mozno to mozes pouzit.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 30. 12. 2011 16:20
Re: Integrál - substituce
Ted jsem to pocital, preklep to neni. Jednoduse si vyjadris cos(x) a sin(x) ze substituce tg(x)=t a dosadis.
Sin(x) treba takhle  a dosadis subsituci. Podobne pak pro cos(x). Vyleze ti racionalni lomena funkce a pak uz jen parcialni zlomky a hotovo.Ted jsem to pocital, preklep to neni. Jednoduse si vyjadris cos(x) a sin(x) ze substit
a dosadis subsituci. Podobne pak pro cos(x). Vyleze ti racionalni lomena funkce a pak uz jen parcialni zlomky a hotovo.Ted jsem to pocital, preklep to neni. Jednoduse si vyjadris cos(x) a sin(x) ze substit
Offline

 , ak
, ak  tak
tak  je vyborna substitucia.
je vyborna substitucia.