Matematické Fórum

janina.kucera · 30. 12. 2011 09:31

Mohla bych prosím poprosit o pomoc s tímto příkladem?

Pro jaká x budou čísla (x-3)/7 , (x-2)/5 a (x-4)/3 současně celými čísly?

Když si položím, že k=(x-3)/7 , l= (x-2)/5 a m= (x-4)/3, pak dostanu 7k+3=5l+2=3m+4. Dostávám teda soustavu diofantovských lineárních rovnic. Ale když to řeším, tak mi vychází, že to nemá řešení, přitom jedno řešení je určitě 52 po dosazení do zadání. Nevím si s tím rady. Děkuju za pomoc

Pavel · 30. 12. 2011 10:26

↑ janina.kucera:

Soustavu vytvoříme takto:

$7k+3&=5l+2\\ 5l+2&=3m+4\\ \\ 7k-5l&=-1\\ 5l-3m&=2.$

Řešení první rovnice - 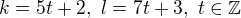$k=5t+2,\ l=7t+3,\ t\in\mathbb{Z}$ .
Řešení druhé rovnice - 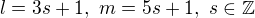$l=3s+1,\ m=5s+1,\ s\in\mathbb{Z}$ .

Odtud vyplývá, že 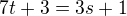$7t+3=3s+1$ , tj. $7t-3s=-2$ . Tato rovnice má řešení

$t=3u+1,\ s=7u+3,\ u\in\mathbb{Z}.$

Odsud obdržíme řešení:

$x=7k+3=7(5t+2)+3=35t+17=35(3u+1)+17=105u+52,\ u\in\mathbb{Z}.$

janina.kucera · 30. 12. 2011 12:17

↑ Pavel: Děkuju moc, všechno mi vyšlo až na t a s. Mě vyšlo, že t= 3u-2 a s=7u-4. To moje je špatně. Když to potom dosadím, abych zjistila x, tak mi to nevychází, ale nevím, co tam teda dělám špatně.

Můj postup: s=(2+7t)/3=2t+(t+2)/3

u=(t+2)/3 potom t= 3u-2 a po dosazení mi vyšlo s= 7u-4

Děkuju

vanok · 30. 12. 2011 12:19

Ahoj ↑ janina.kucera:,
tvoje cvicenie ma vo vseobecnocti taketo skoro poeticke meno "Čínská věta o zbytcích"
a na riesenie tvojho specialneho pripadu mozes pouzit

http://en.wikipedia.org/wiki/Chinese_re … e_solution

kaki1 · 30. 12. 2011 13:05

V tomto případě je Čínská věta o zbytcích zakázána přímo vyučujícím, jinak by řešení bylo velice snadné.

vanok · 30. 12. 2011 13:41 — Editoval vanok (30. 12. 2011 13:41)

Ahoj ↑ kaki1:,
Mala poznamka:ak je to tak preco to nie je napisane v texte cvicenia?
Davat tu neuplne znenia cviceni nie je velmi ferove a ani velmi prodiktivne!

A inac:
Ak niekto napise relacie typu rovnica je uz v Cinskej vete...

Asi potom ostava len napisat pre kazdu relaciu mnozinu cisiel co vyhovuje
A na koniec urobit ich priesek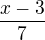
$\frac {x-3} 7$ je cele pre x v $\{..., -4; 3; 10; 17;...\}$
atd...
a ciel cvicenia je asi ukazat "ake je to komplikovane"... A TAK dokazeme .... to co bolo zakazane pouzit.

Pavel · 30. 12. 2011 17:00

↑ janina.kucera:

Výsledek máš dobře, je jen jinak zapsaný. Opravdu t= 3u-2 a s=7u-4 řeší také poslední rovnici. Když je dosadíš za x, dostaneš

$x=7k+3=7(5t+2)+3=35t+17=35(3u-2)+17=105v-53,\ v\in\mathbb{Z}.$

Což je jedno a totéž. Všimni si, že když já ve svém řešení dosadím za u=0, tak je to totéž, jako když Ty dosadíš za v=1. Když já dosadím za u=1, tak Ty dosadíš za v=2. Oba dostaneme stejnou množinu řešení. Platí totiž, že z mého řešení se dostanu na Tvé řešení substitucí u=v-1.

janina.kucera · 30. 12. 2011 17:32

↑ Pavel: Už jsme to vyřešila, děkuju moc, velice mi to pohohlo. Ale jen malé doplnění, když dosadíš tvoje t a s do rovnice, ze které jsi je získal, tak ti to nevyjde, takže jsi tam asi někde udělal chybu.

Pavel · 30. 12. 2011 17:59

↑ janina.kucera:

Pokud dosadím svoje řešení $t=3u+1,\ s=7u+3,\ u\in\mathbb{Z}$ do rovnice $7t-3s=-2$ , dostanu

$7(3u+1)-3(7u+3)&=-2\\ 21u+7-21u-9&=-2\\ -2&=-2.$

Chybu nikde nevidím. Co Ti nevyšlo?

janina.kucera · 30. 12. 2011 18:39

↑ Pavel:Udělala jsem chybu ve znaménku :)

Matematické Fórum

#1 30. 12. 2011 09:31

Diofantovské rovnice

#2 30. 12. 2011 10:26

Re: Diofantovské rovnice

#3 30. 12. 2011 12:17

Re: Diofantovské rovnice

#4 30. 12. 2011 12:19

Re: Diofantovské rovnice

#5 30. 12. 2011 13:05

Re: Diofantovské rovnice

#6 30. 12. 2011 13:41 — Editoval vanok (30. 12. 2011 13:41)

Re: Diofantovské rovnice

#7 30. 12. 2011 17:00

Re: Diofantovské rovnice

#8 30. 12. 2011 17:32

Re: Diofantovské rovnice

#9 30. 12. 2011 17:59

Re: Diofantovské rovnice

#10 30. 12. 2011 18:39

Re: Diofantovské rovnice

Zápatí