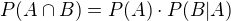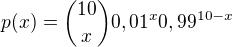Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 12. 2011 18:09
pravděpodobnost
Poradí mně nekdo s těmato příkldama prosím.
Př1: "Ve třídě jsou 2 dívky a 4 chlapci. Jednou za týden jde k tabuli 1 žák, který je náhodně vylosovaný. Tudíž, během 6 týdnů jde každý žák k tabuli. Jaká je pravděpodobnost, že během prvních dvou týdnů pudou k tabuli dívky?"
Př2: Zmetkovistost je v průměru 1%. Jaká je pravděpodobnost, že se mezi 200 výrobky objeví více než 2 zmetky?
Př3: Pravděpodobnost měření je 1%. Kolika chybných měření se dopustíme, jestliže provádíme 10 nezávislých měření?
řešením si nejsu vůbec jistý,ale pokusil sem se o neco...
Offline
- (téma jako vyřešené označil(a) Rufus)
#2 30. 12. 2011 23:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: pravděpodobnost
Zdravím,
pochybuji, že někdo bude si jistý po přečtení Tvé tvorby. Rozděl si to do samostatných témat, prosím, pro zápis použij Editor LaTeXu napravo od okna zprávy. Návrhy řešení okomentuj, prosím, slovně. Viz pravidla a doporučení pro dotaz.
Děkuji.
Offline
#3 31. 12. 2011 13:42 — Editoval pepano (31. 12. 2011 14:30)
Re: pravděpodobnost
Př. 3: Co máte vyřešit? Jestliže provádíme 10 nezávislých měření, tak se nemusíme dopustit žádné chyby, 1 chyby, 2 chyb … i 10 chyb. Vy jste vypočítal pravděpodobnost, že se dopustíme chyby při každém měření. Otázka bude zřejmě znít trochu jinak.
Př. 2: Jedná se o binomické rozdělení. Spočteme si pravděpodobnost, že žádný výrobek není zmetek, pak že jeden výrobek je zmetek a že dva výrobky jsou zmetkové. Sečtením jednotlivých pravděpodobností vypočteme, že mezi 200 výrobky jsou nejvýše 2 zmetky. Pravděpodobnost, že mezi 200 výrobky je více zmetků, než dva je jev opačný, takže pravděpodobnost je zbytek do 1.
Př. 1: Vy jste vypočetl pravděpodobnost, že v prvém týdnu budou vyvolány obě dívky. Ale v prvním týdnu může být vyvolána 1 dívka a v druhém týdnu druhá dívka.
Offline
#4 01. 01. 2012 18:16 — Editoval Rufus (01. 01. 2012 18:18)
Re: pravděpodobnost
↑ pepano:
Děkuji za pomoc. Omlouvám se, že to nepíšu v Latexu, ale nemám na to čas.
Př1: takže mám prvě vypočítat, že se vylosuje jedna dívka ze 6 studentů a k tomu pak přičíst, že se vylosuje dívka z 5 studentů? Nějak tak?
Př2: Děkuju. Už vím jak na to.
Př3: Vypadlo mně slovíčko "chybného". Takže příklad zní takto: Pravděpodobnost chybného měření je 1%. Kolika chybných měření se dopustíme, jestliže provádíme 10 nezávislých měření?
(na tento příklad nevím jak na něho)
Offline
#6 01. 01. 2012 21:43
Re: pravděpodobnost
↑ Rufus:
Je viac sposobov ako vyriesit ten prvy priklad (samozrejme vysledok je vzdy rovnaky). Jeden z nich ti uz napisal kolega pepano s pouzitim podmienenej pravdepodobnost, ale da sa to vyriesit aj bez toho, dokonca aj bez kombinacnych cisel.
Ak predpokladame, ze vzdy je vyvolany student, ktory este pri tabuli nebol, tak prvy tyzden mozeme vyvolat siestich, druhy uz iba piatich atd., pricom posledny student uz nie je vyvolany nahodne, ale je to ten student, ktory za prvych 5 tyzdnov pri tabuli nebol. Cize celkovy pocet takych postupnosti, ze v akom poradi mohli ti studenti ist odpovedat je 6.5.4.3.2.1 = 6! = 720.
Teraz nas zaujima pocet takych postupnosti, v ktorych su na prvych dvoch miestach dievcata. Ak si dievcata oznacime ako A,B, tak taketo postupnosti mozu zacinat bud AB alebo BA. To su 2 moznosti, pricom ku kazdej z nich mozeme lubovolne zoradit zvysnych 4 chlapcov. Chlapcov takto zoradime 4! sposobmi, takze celkovy pocet takych postupnosti ktore zacinaju dievcatami je 2.4! = 2.24 = 48.
Teraz uz len vypocitame pravdepodobnost ako podiel tych postupnosti zacinajucich dievcatami zo vsetkych moznych postupnosti, teda 48/720, co je 1/15.
Offline
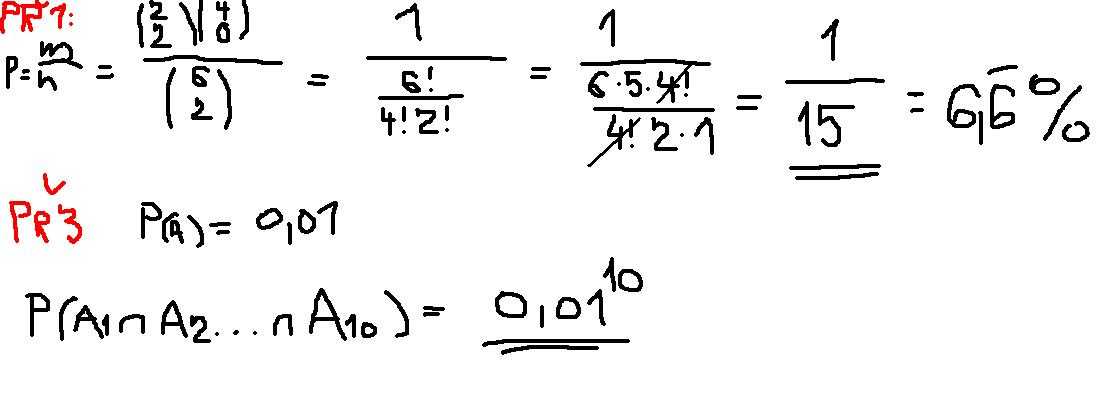

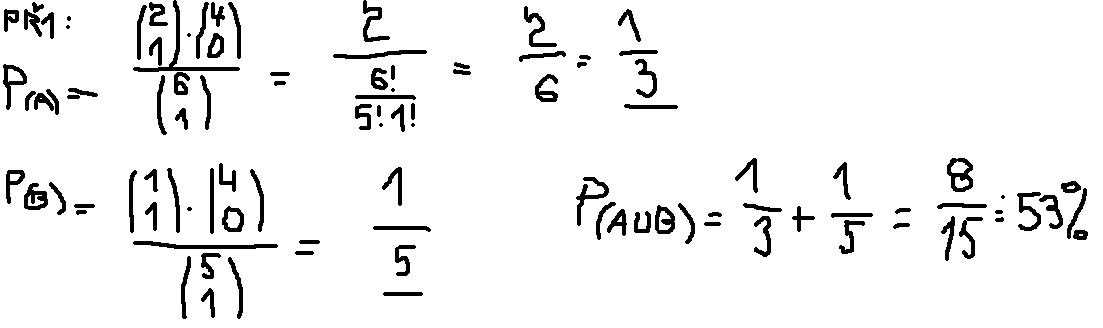
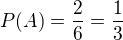
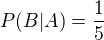 za podmínky, že v prvém týdnu byla vyvolána dívka
za podmínky, že v prvém týdnu byla vyvolána dívka