Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 01. 2012 21:25
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Nehomogenní diferenciální rovnice - důkaz
Dobrý večer, zajímalo by mě, jak dokážu rovnost: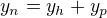
přičemž  je obecné řešení nehomogenní lineární diferenciální rovnice,
je obecné řešení nehomogenní lineární diferenciální rovnice, 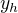 je o.ř. odpovídající homogenní rovnice a
je o.ř. odpovídající homogenní rovnice a 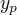 je partikulární řešení této nehomogenní LDR?
je partikulární řešení této nehomogenní LDR?
mělo by to asi vyplívat z věty, která říká že rozdíl dvou partikulárních řešení NLDR je řešením HLDR (kterou umím dokázat). Je možné že to mám před očima a jen nejsem schopný přijít na závěrečný krok.
Díky:)
Offline
#2 04. 01. 2012 01:38
Re: Nehomogenní diferenciální rovnice - důkaz
Zdravím,
vďaka tomu že množina všetkých riešení HLDR tvorí konečnorozmerný vektorový priestor nad  dimenzie n (a teda aj podpriestor reálnych priestorov vyšších dimenzií) si myslím že sa "môžme hrať" na jednoznačné bázické aj afinné súradnice, potom vyjadrenie
dimenzie n (a teda aj podpriestor reálnych priestorov vyšších dimenzií) si myslím že sa "môžme hrať" na jednoznačné bázické aj afinné súradnice, potom vyjadrenie 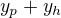 by malo byť parametrickým vyjadrením afinného podpriestoru
by malo byť parametrickým vyjadrením afinného podpriestoru  všetkých riešení tejto NLDR, o ktorom by už nemal byť problém ukázať že ho odčítaním/pričítaním partikulárneho riešenia vieme "posunúť" do nuly a zasa späť
všetkých riešení tejto NLDR, o ktorom by už nemal byť problém ukázať že ho odčítaním/pričítaním partikulárneho riešenia vieme "posunúť" do nuly a zasa späť
možno by si mohol skúsiť teraz vziať ľubovoľné 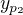 z množiny všetkých riešení NLDR a a napísať si ho v tvare
z množiny všetkých riešení NLDR a a napísať si ho v tvare  (pričom to
(pričom to 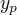 je samozrejme partikulárne riešenie ktoré už máš ) ..
je samozrejme partikulárne riešenie ktoré už máš ) ..
podľa toho čo si spomenul že vieš dokázať už vieš že tá zátvorka je riešením príslušnej HLDR
ešte chcem povedať že to čo som tu napísal som neoveril, takto sa mi to javí z hľadiska lineárnej algebry, a okrem toho je dosť neskoro večer, takže bude dobré ak si to najprv ešte rozmyslíš ;-)
Offline
#3 04. 01. 2012 10:23 — Editoval Rumburak (04. 01. 2012 15:17)
Re: Nehomogenní diferenciální rovnice - důkaz
↑ Sam_Hawkins:
Také zdravím. Principem, který k tomuto výsledku vede, je opravdu jen linearita, jak již naznačil kolega ↑ jardofpr:.
Snadno nahlédnme, že platí věta
Jsou-li 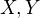 lineární prostory,
lineární prostory, 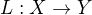 lineární zobrazení a
lineární zobrazení a  takové, že
takové, že 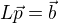 , potom
, potom
(1)  .
.
Formuli
 z (1) můžeme vyjádřit ve tvaru
z (1) můžeme vyjádřit ve tvaru  neboli
neboli  , kde
, kde 
je tzv. jádro linárního zobrazení L .
Offline

 je ekvivalentní s rovnicí
je ekvivalentní s rovnicí 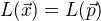 .
.