Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 04. 01. 2012 18:23 — Editoval vanok (04. 01. 2012 18:28)
Re: Rovnice o jedné neznámé
Ahoj ↑ Tue09:,
najprv to treba zjednodusit
Toto: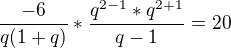
je ekvivalente z 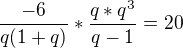
a este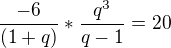
a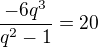
Dokazes pokracovat?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 04. 01. 2012 18:35
Re: Rovnice o jedné neznámé
Omlouvám se, ta rovnice je špatně zadána 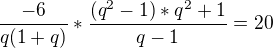
Tato je správně
Mohl byste prosím vypracovat nějaký postup? Já se dostal k fázi, kde mi vyjde, že ta rovnice je kubická, což je asi špatně, protože jsme to ještě nebrali, myslím tedy, že tam mám někde chybu.
Offline
#4 04. 01. 2012 18:38
Re: Rovnice o jedné neznámé
↑ Tue09:,
no ale sa mi zda ze tam este chyba jedna zatvorka:
Nie je to skor takto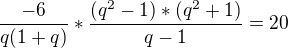 ?
?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 05. 01. 2012 03:23 — Editoval vanok (05. 01. 2012 03:34)
Re: Rovnice o jedné neznámé
Ahoj ↑ jelena:,
Co pises je pravda, ale je lepsie zjednodusit tento vyraz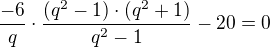
co da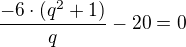 pre
pre 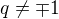
a potom 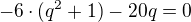 ak naviac
ak naviac 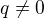
alebo este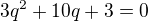
Ktoru kolega Tue09 hravo vyriesi a urobi skusku v jeho prvej SPRAVNEJ rovnici
A potom vysvetli preco nemozeme mat
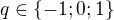
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

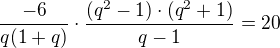 potom převedu na anulovaný tvar a také upravím jmenovatel
potom převedu na anulovaný tvar a také upravím jmenovatel 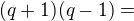 ...
...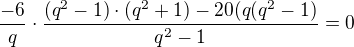
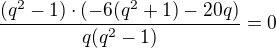 to uz se podaří -
to uz se podaří -