Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 01. 2012 13:48
Rovina symetrie různoběžných rovin
Mám vypočítat tento příklad a vůbec si nevím rady :((
Najděte roviny symetrie různoběžných rovin:
ρ1: 2x + 5y - 5z + 16 = 0
ρ2: 2x – 7y – z + 8 =0
Jediné co mě napadlo je vypočítat jejich průsečík, ale nevím
Děkuju za každou radu
Offline
#2 04. 01. 2012 15:24
Re: Rovina symetrie různoběžných rovin
Ahoj ↑ Peggy1012:,
JA vzdy najprv pozdravim a ty?
Tie roviny symetrie su vlastne analogie z rovinym problemom
osy dvoch nerovnobeznych priamok .
A mozes nam napisat ako su geometricky urcene taketo roviny v tvojom pripade?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 04. 01. 2012 15:31
Re: Rovina symetrie různoběžných rovin
Roviny v R3 , pokud nejsou rovnoběžné, mají průsečnici (nikoliv průsečík).
Zkusil bych vyšetřovat množinu všech koulí, které mají dotyk s každou z obou daných rovin.
Středy těchto koulí vyplní obě hledané roviny semetrie těchto rovin.
Offline
#4 04. 01. 2012 15:46
Re: Rovina symetrie různoběžných rovin
↑ vanok:
Ahoj vanok,
Omlouvám se za vynechání pozdravu, nebylo to úmyslem.
tak mě napadá, nešlo by to přes určení nějaký bodů na přímkách a pak vypočítat jejich středy ???
Jinak opravdu netušímmmm :(
Děkujuu za každou radu
Offline
#5 04. 01. 2012 15:48
Re: Rovina symetrie různoběžných rovin
↑ Rumburak:
Ahojda,
a mohl bys mi prosím nastínit kousek řešení, páč vůbec netušímmm
Děkujuu za každou radu
Offline
#6 04. 01. 2012 16:06
Re: Rovina symetrie různoběžných rovin
↑ Peggy1012:↑ Peggy1012:,
kolega ti dal dobru myslienku na najdenie bodov mimo priamku co su rovnako vzdialene od dvoch danych rovin. Vyuzi to!
A potom, ked to urobis porozmyslame ci takto mas vsetki roviny co hladas.( to je ta otazka kolko je takychto rovin?)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 04. 01. 2012 16:48
Re: Rovina symetrie různoběžných rovin
↑ Peggy1012:,
alebo spolocna priamka rovin ako ti uz napisal kolega↑ Rumburak:,
a jeden stred nejakej z tych gul urci taku rovinu
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 04. 01. 2012 17:06 — Editoval Rumburak (04. 01. 2012 17:09)
Re: Rovina symetrie různoběžných rovin
↑ Peggy1012:
I. Nástin analytického řešení.
Nechť S[u, v, w] je střed takové koule K a r >= 0 její poloměr (budeme připouštět i koule, které zdegenerují do jediného bodu,
proto připouštíme možnost r = 0). Rovnice koule pak bude
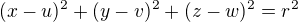 .
.
Bod jejího dotyku s první rovinou nechť je ![kopírovat do textarea $A[x,y,z]$](/mathtex/51/5137ec30272ce28147c292bc6ce9180a.gif) , bod dotyku s druhou rovinou nechť je
, bod dotyku s druhou rovinou nechť je ![kopírovat do textarea $B[\xi,\eta,\zeta]$](/mathtex/7f/7fa8042f8c71dbb743f535ff0adb974f.gif) .
.
Celkem tedy musí být splněna soustava rovnic
(1)  ,
,
 ,
,

s neznámými 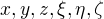 a parametry
a parametry  . Cílem je nalézt fomuli
. Cílem je nalézt fomuli  , jejíž splnění bude ekvivalentní s výrokem,
, jejíž splnění bude ekvivalentní s výrokem,
že soustava (1) má jediné řešešení. Z formule  pak odvodíme rovnice hledaných rovin symetrie.
pak odvodíme rovnice hledaných rovin symetrie.
II.
Ale předchozí postup odhaduji jako velmi pracný. Dalo by se využít, že průsečnice p daných rovin je i průsečnicí hledaných rovin a pak tedy k určení
každé z nich postačí nalézt pouze jeden její bod ležící mimo přímku p . Takovým bodem bude střad úsečky AB , kde B je dvojice navzájem
symetrických bodů (neležících v přímce p). Postačí zvolit v jedné rovině bod A mimo přímku p, k němu nalézt bod B v druhé rovině tak, aby
byl rovinně symetrický s bodem A , tj. aby na přímce p ležel bod P s vlastnostmi
1. přímky PA , PB jsou kolmé k přímce p,
2. |PA| = |PB| .
Pro bod B budou existovat 2 řešení a každé z nich dá pomocí postupu uvedeného na začátku odstavce II. jednu rovinu symetrie.
Zde ale zase bude problém s důkazem, že jsme úlohu vskutku vyřešili, a to vyčerpávajícím způsobem.
Offline
#10 04. 01. 2012 17:16
Re: Rovina symetrie různoběžných rovin
Ahoj ↑ Rumburak:,
Ano, ale co povedat o rovinach co su kolme na priesecnicu danych rovin?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 05. 01. 2012 10:38
Re: Rovina symetrie různoběžných rovin
Ahoj ↑ vanok: ,
Úlohu jsem chápal tak, že hledáme takové rovinné symetrie, které rovinu ρ1: 2x + 5y - 5z + 16 = 0
zobrazují na rovinu ρ2: 2x – 7y – z + 8 =0 (a naopak). Máš pravdu, že zadání se dá vyložit i šířeji -
- tak, jak naznačuješ.
Offline

