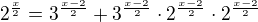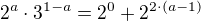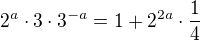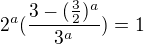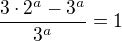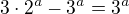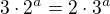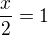Matematické Fórum

Anonymystik · 05. 01. 2012 16:26

Zdravím. Mám následující exponenciální rovnici: 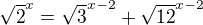$\sqrt{2}^{x}= \sqrt{3}^{x-2} + \sqrt{12}^{x-2}$ . Přinesla mi ji kamarádka ze školy s tím, že prý to dostala jako příklad za jedničku. Tak jsem si říkal, že to bude jednoduché. Postupně jsem na to vyzkošel všechny finty, jako je logaritmování, substituce, převádění na společný základ, rozkládání na součin závorek atd., jenže výsledek se (světe div se) nedostavil. Jediné, co vím, je, že jediné řešení má být x=2 (podle WolframAlpha), což lze snadno ověřit. Ovšem jak k tomuto výsledku lze dojít, aniž bych ho uhodl? Díky za každou smysluplnou radu.

Jan Jícha

Jen tak mě napadla taková věc. (Jsem jen obyčejný čtvrťák, takže když to bude nějaká hloupost, předem se omlouvám - to Vy jste tu matematická kapacita!) :))

Převedl bych si to na $2^{\frac {x}{2}}=3^{\frac{x-2}{2}}+12^{\frac{x-2}{2}}$

Dále upravil na 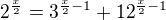$2^{\frac {x}{2}}=3^{\frac{x}{2}-1}+12^{\frac{x}{2}-1}$

Substituce za 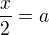$\frac{x}{2}=a$

Dostanu 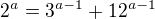$2^{a}=3^{a-1}+12^{a-1}$
A to by nešlo nějak rozumně vyřešit?

Anonymystik · 05. 01. 2012 17:49

↑ Honza Matika: Právě že do tohoto tvaru jsem to taky dostal. Ještě jsem si dokonce zavedl substituce $u=2^{a}, v=3^{a}$ , ale ani s tím jsem nijak nepohnul.

xfastx · 05. 01. 2012 19:38

Dostanu $2^{a}=3^{a-1}+12^{a-1}$
A to by nešlo nějak rozumně vyřešit?

Zkusil bych tu rovnici zlogaritmovat

Jan Jícha · 05. 01. 2012 20:26

↑ xfastx: Já jí logaritmoval asi deset krát. Jenom asi nemám den, nebo je to nad moje síly.:)

smatel · 05. 01. 2012 20:36

↑ Honza Matika:

Já s tím dělal taky všechny psí kusy, trošku mě vadí, že tam jako poslední člen vychází ta dvanáctka, jako základ, kdyby tam tam byla šestka, bylo by to lepší..

Jan Jícha

↑ smatel: Tak když mi to vypočítáš se šestkou na konci (místo té dvanáctky), dám Tě osobně pět plusových karma bodů :)))

Edit: Tím jsem chtěl říct, že IMHO si tím vůbec nepolepšíš.

halogan

Nebylo určeno, z jakého oboru mají být $x$ ? Protože jako diofantická rovnice je

$2^{a}=3^{a-1}+12^{a-1}$

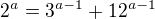
celkem jednoduchá.

Edit: tak mám i řešení pro 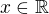$x \in \mathbb{R}$ .

Stačí si to přepsat jako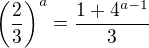

$$\frac 23$^a = \frac{1+ 4^{a-1}}{3}$ .

Vlevo máme ryze klesající funkci, vpravo ryze rostoucí. Jediný kořen najdeme, pokud se omezíme na celá čísla a dál viz výše. Moc učesané to není, ale k výsledku to vede.

Snad tam nemám nějakou botu.

smatel · 05. 01. 2012 20:59

↑ Honza Matika:Beru zpět, i když nabídka je to lákavá. Trošku jsem se nechal zmámit, jednou jsem řešil podobný případ a tam stačilo podělit rovnici součinem obou mocnin základů, tady to pravděpodobně nelze:-( Pardon za zmatek.

Anonymystik · 05. 01. 2012 22:59

↑ halogan: Děkuji. K něčemu podobnému jsem taky dospěl, dokázal jsem, že to má nejvýše 1 kořen a ten jsem uhodl. Ale připadá mi, že ničeho lepšího se u téhle rovnice nedopídíme.
↑ smatel: Je to přesně tak, kdyby tam byla šestka místo dvanáctky, šlo by to krásně algebraicky upravit na součin a nebyl by problém. Možná se kamarádky ještě zeptám, jestli nespletla zadání. Výsledek sice vyjde úplně stejně, ale typově je to pak úplně jiná úloha (resp. její řešení je zcela odlišné).

Každopádně všem moc děkuji.

halogan · 06. 01. 2012 10:28

↑ gogy27:

Anonymystik napsal(a):
Jediné, co vím, je, že jediné řešení má být x=2 (podle WolframAlpha), což lze snadno ověřit. Ovšem jak k tomuto výsledku lze dojít, aniž bych ho uhodl?

gogy27 · 06. 01. 2012 11:31 — Editoval gogy27 (06. 01. 2012 11:32)

$\sqrt{2}^{x}= \sqrt{3}^{x-2} + \sqrt{12}^{x-2}$
$2^{\frac {x}{2}}=3^{\frac{x-2}{2}}+12^{\frac{x-2}{2}}$
$2^{\frac {x}{2}}=3^{\frac{x-2}{2}}+3^{\frac{x-2}{2}}\cdot 2^{\frac{x-2}{2}} \cdot 2^{\frac{x-2}{2}}$
$2^{\frac {x}{2}}=3^{\frac{x-2}{2}}\cdot (1+2^{\frac{x-2}{2}} \cdot 2^{\frac{x-2}{2}})$
$\frac{2^{\frac {x}{2}}}{3^{\frac{x-2}{2}}}= 1+2^{\frac{x-2}{2}} \cdot 2^{\frac{x-2}{2}}$
$\frac{x}{2} = a$
$2^{a}\cdot {3^{1-a}} = 2^{0}+2^{2\cdot (a-1)}$
$2^{a}\cdot 3\cdot 3^{-a} =1+2^{2a} \cdot \frac{1}{4}$
$2^{a}\cdot 3\cdot 3^{-a} - 2^{a}\cdot 2^{a} \cdot \frac{1}{4} =1$
$2^{a} (3\cdot 3^{-a} - 2^{a} \cdot \frac{1}{4}) =1$
$2^{a} (\frac{3}{3^{a}} - \frac{2^{a}}{4}) =1$
$2^{a} (\frac{12 - 6^{a}}{4\cdot 3^{a}}) =1$
$2^{a} (\frac{3 - (\frac{3}{2})^{a}}{3^{a}}) =1$
$2^{a} (\frac {\frac{3\cdot 2^{a}-3^{a}}{2^{a}}}{3^{a}}) =1$
$\frac{3\cdot 2^{a}-3^{a}}{3^{a}} =1$
$3\cdot 2^{a}-3^{a} =3^{a}$
$3\cdot 2^{a} =2\cdot 3^{a}$
$\frac{3}{2}=\frac{3^{a}}{2^{a}} \Rightarrow a = 1$
$\frac{x}{2} = a$
$\frac{x}{2} = 1$
$x=2$

Trosku nepriehladne ale snazil som sa to robit krocik po krociku. Snad pochopite.

halogan · 06. 01. 2012 11:35

$2^{a} (\frac{12 - 6^{a}}{4\cdot 3^{a}}) =1$

$2^{a} (\frac{3 - (\frac{3}{2})^{a}}{3^{a}}) =1$

Co to je za upravu?

rleg · 06. 01. 2012 13:56

vynásobil zlomek $\frac44$

halogan · 06. 01. 2012 13:58

↑ rleg:

To by tam nedostal (3/2)^a.

smatel · 06. 01. 2012 14:14

↑ rleg:
Ne to je blbě. Tam se nedopatřením ta čtyřka dostala do základu mocniny a ještě se ten zlomek pokrátil. Tudy cesta nevede, ale je zajímavé že to vyšlo :D

gogy27 · 06. 01. 2012 15:45 — Editoval gogy27 (06. 01. 2012 15:46)

Áno áno, priznávam, je tam chyba. Tak som to skúsil inou cestou a vyšlo mi akurát, že $a\in (-\infty ,1>$ a teda $x\in (-\infty ,2>$
Na základe tohto:

$2^{a} (\frac{3}{3^{a}} - \frac{2^{a}}{4}) =1$
$\frac{3\cdot 2^{a}}{3^{a}} - \frac{(2^{a})^{2}}{4} =1$
$\frac{4\cdot 3\cdot 2^{a}-(2^{a})^{2}\cdot 3^{a}}{4\cdot 3^{a}} =1$
$4\cdot 3\cdot 2^{a}-(2^{a})^{2}\cdot 3^{a} =4\cdot 3^{a}$
$(2^{a})^{2}\cdot 3^{a} - 4\cdot 3\cdot 2^{a}+4\cdot 3^{a}=0$

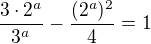
Teda kvadratická rovnica a odtiaľ: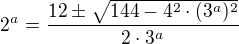
$2^{a} = \frac{12 \pm \sqrt{144 - 4^{2}\cdot (3^{a})^{2}}}{2\cdot 3^{a}}$
$2^{a} = \frac{12 \pm 4\cdot \sqrt{9 - (3^{a})^{2}}}{2\cdot 3^{a}}$
$2^{a} = \frac{6 \pm 2\cdot \sqrt{9 - (3^{a})^{2}}}{3^{a}}$
$2^{a} = \frac{2\cdot (3\pm \sqrt{(3 - 3^{a})(3+3^{a})}}{3^{a}}$

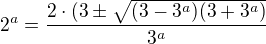
Vieme, že pod odmocninou nesmie byť záporné číslo teda $3-3^{a} \ge 0 \Rightarrow 3\ge 3^{a} \Rightarrow a\le 1$ Z toho vyplýva, že $2^{a} \le 2$ a vieme, že $2^{a} > 0$

Ale ďalej som už bezbranný :D

peter_2+2

↑ smatel:

:D taky čučím, ale už jsem nato došel, jsem se tam zapletl, původně jsem myslel, že zaměnil 4 za 2^a, kdo se v tom má vyznat :).

On tam hodil tu 4ku jako 4^a, a "a" je 1, takže je to ok, zkrátka už tušil, kolik to má vyjít :).

Jinak já bych tu substituci asi udělal takto spíš:
$a=\frac{x}{2}-1$

$2*2^{\frac{x}{2}-1}=3^{\frac{x}{2}-1}+12^{\frac{x}{2}-1}$

Ikdyž ono to je asi jedno.

Já zase tak moc nerozumím iracionálním číslům, ale fakt je ten, že mocninou celého čísla vznikne vždy celé číslo a mocninou zlomku(pokud samozřejmě nejde o zlomek typu 4/2, což je celé číslo) vyjde vždy zlomek, což lze snadno dokázat i u zlomků, že vzájemná nedělitelnost prvočísel např. 3/2 se nezmění ani po zmnožení jejich počtu, např. (3*3)/(2*2), tedy i po umocnění vyjde zlomek.

Čili pokud by se hned o začátku vycházelo z toho, že mocnina musí být celé číslo, určitě by to hledání netrvalo příliš dlouho, a došlo by se na to, že exponent musí být menší než jedna =>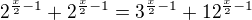
$2^{\frac{x}{2}-1}+2^{\frac{x}{2}-1}=3^{\frac{x}{2}-1}+12^{\frac{x}{2}-1}$

Nevím jak moc toho matematika ví o sčítání dvou iracionálních čísel a o možnosti dát stejný výsledek(ono stejně v tomto případě nic jiného než nula vyjít nemůže, ale myslím tím obecně), nejde samozřejmě ani vyloučit, že součet dvou iracionálních čísel nedá vznik číslu racionálnímu apod. V každém případě nalevo pokud by bylo iracionální číslo, pak by šlo o iracionální číslo, které vzniklo z násobků 2ky (např. sqrt(2) ) a napravo z 3ky/12tky, podle mě to asi ani pomocí iracionálních rovnic nejde řešit, ale já o iracionálních rovnicích toho zas tak moc nevím, podle mě v nich jde stejně jen oto, že se např. sqrt(2)*sqrt(2) zruší nebo že sqrt(2)/sqrt(2) se podělí, ale kdybych tvrdil, že to tak je určitě tak bych lhal.

Každopádně by mě zajímalo, jestli se to dá vyřešit nějakým běžným způsobem(bez kvadratické rovnice apod.), já jsem se do toho moc nepouštěl, a tadyhle gogy vypadá v řešení exponencionálních rovnic víc než zdatnej, takže se oto rači ani pokoušet nebudu :)), asi by se muselo zrušit sčítání a pak převést na stejný základ, to je ale tady zhola nemožné podle mě, zlogaritmovat to, to podle mě taky nic neřeší, tím se rovnice jen převede na úpravu, kdy se navzájem rovnají exponenty mocnin, které se samozřejmě rovnají, pokud se rovnají mocniny samy, což je to samé jako to koneckonců převést na stejný základ a základu se nakonci zbavit. Takže asi leda tu kvadratickou rovnici.

Ještě by se stím dalo udělat toto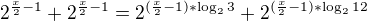
$2^{\frac{x}{2}-1}+2^{\frac{x}{2}-1}=2^{(\frac{x}{2}-1)*\log_2{3}}+2^{(\frac{x}{2}-1)*\log_2{12}}$

$2^{a}+2^{a}=2^{a*\log_2{3}}+2^{a*\log_2{12}}$

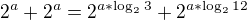
Kde výsledky těch logaritmů by byly znovu iracionální, takže by se stejně nenašlo přesný řešení, ale jen přibližný. Ale v tomto případě by to asi stačilo, když by se řeklo, že protože oba výsledky těch logaritmů představují množství větší než 1dna a oba mají stejné znaménko, tak by se mělo dát napsat: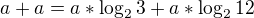
$a+a=a*\log_2{3}+a*\log_2{12}$
Tady by bylo taky vidět, že a=0 a že x=2

Kondr · 03. 05. 2012 17:30

Co tohle:

$\sqrt{2}^{x}= \sqrt{3}^{x-2} + \sqrt{12}^{x-2}$
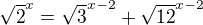
přepíšeme na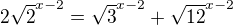
$2\sqrt{2}^{x-2}= \sqrt{3}^{x-2} + \sqrt{12}^{x-2}$
užitím vztahu 2=1+1 a distributivity násobení
$\sqrt{2}^{x-2}+\sqrt{2}^{x-2}= \sqrt{3}^{x-2} + \sqrt{12}^{x-2}$ (1)
Pro $x>2$ je $\sqrt{2}^{x-2}<\sqrt{3}^{x-2}$ a $\sqrt{2}^{x-2}<\sqrt{12}^{x-2}$ , tedy v (1) je levá strana menší než pravá.
Pro $x<2$ je $\sqrt{2}^{x-2}>\sqrt{3}^{x-2}$ a $\sqrt{2}^{x-2}>\sqrt{12}^{x-2}$ , tedy v (1) je levá strana větší než pravá.
Pro $x=2$ máme řešení.

EK · 28. 12. 2012 00:59

Podle mého názoru je možné řešit problém pomocí kvadratické rovnice:

1) Předpokládám (a snad umím i zdůvodnit), že rovnice má jedno řešení.
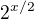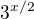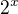2) Upravím, po úpravě mám členy s $2^{x/2}$ , $3^{x/2}$ a $2^{x}$ . Mám tedy kvadratickou rovnici pro 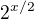$2^{x/2}$ ve které 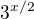$3^{x/2}$ se vyskytuje jako koeficient u kvadratického členu a absolutní člen.
3) Protože předpokládám jedno řešení musí být diskriminant této kvadratické rovnice roven 0. V diskriminantu figuruje člen 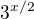$3^{x/2}$ a jsem tudíž schopen určit x (vychází 2).

Pro pokročilou hodinu jsem nezacházel do detailů, pokusím se poslat detailnější řešení co nejdříve.

EK · 01. 01. 2013 22:45

Zde je detailní postup řešení.

1) Na levé a pravé straně rovnice jsou funkce, řešením rovnice je hodnota x pro které je hodnota funkce na levé straně stejná jako hodnota funkce na pravé straně. Obě funkce jsou rostoucí => jedno řešení.
2) Provedu úpravy: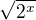
$\sqrt{2^{x}}$ = $2^{x/2}$
$\sqrt{3^{x-2}}$ = $3^{x/2}/3$
$\sqrt{12^{x-2}}$ = $\sqrt{(3*4)^{x-2}}$ = $\sqrt{3^{x-2}*4^{x-2}}$ = $\sqrt{(3^{x}/3^{2})*(4^{x}/4^{2})}$ = $\sqrt{(3^{x}/3^{2})*(2^{2x}/4^{2})}$ = $(3^{x/2}/3)*(2^{x/2}/4)$
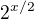
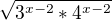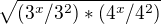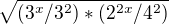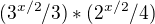
3)Provedu následujicí substituci:
$Y = 2^{x/2}$
$K = 3^{x/2}$
po které:
$\sqrt{2^{x}} = Y$
$\sqrt{3^{x-2}} = 3^{x/2}/3 = K/3$
$\sqrt{12^{x-2}} = (3^{x/2}/3)*(2^{x/2}/4) = Y^{2}*K/12$
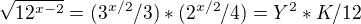
Původní rovnice má potom tvar: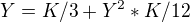
$Y=K/3 + Y^{2}*K/12$
což je kvadratická rovnice: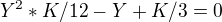
$Y^{2}*K/12 - Y + K/3 = 0$
4) Dle bodu jedna požaduji jedno řešení a tedy diskriminant D teto kvadratické rovnice musí byt 0:
$D = (-1^{2}) - 4*(K/12)*(K/3) = 0$
$1 - 4*K^{2}/36 = 0$
$K^{2}=9$
a tedy K = 3 nebo K = -3
5) Ze substituce $K = 3^{x/2}$ mám pro K = 3:
$3^{x/2}=3$
$x/2 = 1$
$x = 2$
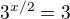
Pro druhou hodnotu K = -3 mám
$3^{x/2}=-3$
které nevyhoví žádné realné číslo.
Řešením je tudíž x = 2.

Tento příklad je ze sbírky:
Jirásek,Braniš,Horák,Vacek: Sbírka úloh z matematiky pro SOŠ a studijní obory SOU. 1.část.
str.284 8.115 a). Ostatní příklady v 8.115 b)-g) jsou pomerně jednoduché (dají se skoro počítat z hlavy) a to mi vede k názoru, že výše uvedené řešení není optimální tj. že musí byt jiný jednodušší způsob.

Jan Jícha · 01. 01. 2013 22:56

↑ EK: Ahoj, postup jsem nekontroloval, ani netvrdím, že je špatně, jen si myslím, že tvoje rovnost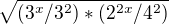
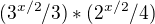$\sqrt{(3^{x}/3^{2})*(2^{2x}/4^{2})}$ = $(3^{x/2}/3)*(2^{x/2}/4)$ neplatí.

IMHO by tam mělo být $2^x$ ... Ale to je jen technická poznámka, možná to na řešení nemá vliv.

Hanis · 02. 01. 2013 00:14

Ahoj,
jen chci poznamenat, že obecný algoritmus pro řešení exponenciální rovnice neexistuje, na rozdíl od lineárí, kvadratické apod.

Uhádnout kořen a ukázat, že je jediným kořenem je naprosto legitimní řešení takovéto úlohy.

Emca21 · 02. 01. 2013 00:19

↑ Hanis:
To jsem nevedel. Zajimave. Takze, kdyz jde videt hned na zacatku, ze reseni je x=2 a ja napisu napr. do testu jenom x=2, potvrdim zkouskou, tak mi nikdo nemuze rict nic?

Matematické Fórum

#1 05. 01. 2012 16:26

Neřešitelná exponenciální rovnice

#2 05. 01. 2012 17:41 — Editoval Honza Matika (05. 01. 2012 17:42)

Re: Neřešitelná exponenciální rovnice

#3 05. 01. 2012 17:49

Re: Neřešitelná exponenciální rovnice

#4 05. 01. 2012 19:38

Re: Neřešitelná exponenciální rovnice

#5 05. 01. 2012 20:26

Re: Neřešitelná exponenciální rovnice

#6 05. 01. 2012 20:36

Re: Neřešitelná exponenciální rovnice

#7 05. 01. 2012 20:40 — Editoval Honza Matika (05. 01. 2012 20:41)

Re: Neřešitelná exponenciální rovnice

#8 05. 01. 2012 20:44 — Editoval halogan (05. 01. 2012 20:48)

Re: Neřešitelná exponenciální rovnice

#9 05. 01. 2012 20:59

Re: Neřešitelná exponenciální rovnice

#10 05. 01. 2012 22:59

Re: Neřešitelná exponenciální rovnice

#11 06. 01. 2012 10:22 Příspěvek uživatele gogy27 byl skryt uživatelem byk7. Důvod: spam

#12 06. 01. 2012 10:28

Re: Neřešitelná exponenciální rovnice

Anonymystik napsal(a):

#13 06. 01. 2012 11:31 — Editoval gogy27 (06. 01. 2012 11:32)

Re: Neřešitelná exponenciální rovnice

#14 06. 01. 2012 11:35

Re: Neřešitelná exponenciální rovnice

#15 06. 01. 2012 13:56

Re: Neřešitelná exponenciální rovnice

#16 06. 01. 2012 13:58

Re: Neřešitelná exponenciální rovnice

#17 06. 01. 2012 14:14

Re: Neřešitelná exponenciální rovnice

#18 06. 01. 2012 15:45 — Editoval gogy27 (06. 01. 2012 15:46)

Re: Neřešitelná exponenciální rovnice

#19 29. 04. 2012 19:18 — Editoval peter_2+2 (29. 04. 2012 20:17)

Re: Neřešitelná exponenciální rovnice

#20 03. 05. 2012 17:30

Re: Neřešitelná exponenciální rovnice

#21 28. 12. 2012 00:59

Re: Neřešitelná exponenciální rovnice

#22 01. 01. 2013 22:45

Re: Neřešitelná exponenciální rovnice

#23 01. 01. 2013 22:56

Re: Neřešitelná exponenciální rovnice

#24 02. 01. 2013 00:14

Re: Neřešitelná exponenciální rovnice

#25 02. 01. 2013 00:19

Re: Neřešitelná exponenciální rovnice

Zápatí