Matematické Fórum

Blujacker · 13. 09. 2008 23:09

ahoj

Snazim se poradne pochopit rozkladani cisel na soucin prvocisel a moc nechapu metodu trial divison
trial division
Na zacatku musim mit nejaky seznam prvocisel, ale nejsem si moc jisty, jak velky by ten seznam mel byt. Aby algoritmus fungovat, staci najit vsechna prvocisla do cisla n, ale to je zbytecne moc prvocisel. Nekde jsem cetl, ze staci najit prvocisla do $\sqrt{n}$ , ale to ne vzdy funguje.
Myslim, ze vzdy bude fungovat, pokud najdu prvocisla do 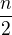$\frac{n}{2}$ , ale neni to zbytecne moc prvocisel?

ps: jak byste prelozili trial division do cestiny?

dik

Lishaak · 13. 09. 2008 23:18

Staci skutecne zkouset prvocisla pouze mensi nebo rovna $\sqrt{n}$ . Zadny delitel cisla 'n' prece nemuze byt vetsi nez $\sqrt{n}$ . Cili vsechna prvocisla, ktera deli 'n' musi byt mensi nebo rovna $\sqrt{n}$ .

Mimochodem, slovnik na www.seznam.cz rika, ze 'trail divisor' je 'zkušební dělitel'...

Pavel Brožek

↑ Blujacker:

Tato metoda spočívá v tom, že zkusíš číslo n vydělit všemi prvočísly menšími nebo rovnými $\sqrt n$ . Pokud žádné prvočíslo menší nebo rovno $\sqrt n$ číslo n nedělí, pak je n prvočíslo. Ukážu to sporem:

Předpokládejme, že n je složené číslo a žádné prvočíslo menší nebo rovno $\sqrt n$ nedělí n. Existují tedy přirozená čísla $p>\sqrt n,\,q>\sqrt{n}$ taková, že $pq=n$ . Zřejmě ale platí

$pq>\sqrt{n}\cdot\sqrt{n}=n$ což je spor.

Marian · 13. 09. 2008 23:52

↑ Lishaak:
Bylo by to třeba upřesnit, protože není pravda, že žádný dělitel přirozeného čísla n není větší než $\sqrt{n}$ . Jenže je nutno pamatovat na to, že i samotné číslo n je taktéž dělitelem čísla n. Takže chybí mi tam u tebe slovíčko "netriviální (dělitel)". Ale úmysl tvého příspěvku byl určitě myšlen správně.

U BrozekP je to formulováno správně.

Lishaak · 14. 09. 2008 00:31

Zatra, tohle me nemelo uniknout, ponauceni vzato...

Matematické Fórum

#1 13. 09. 2008 23:09

trial divison

#2 13. 09. 2008 23:18

Re: trial divison

#3 13. 09. 2008 23:20 — Editoval BrozekP (14. 09. 2008 00:01)

Re: trial divison

#4 13. 09. 2008 23:52

Re: trial divison

#5 14. 09. 2008 00:31

Re: trial divison

Zápatí