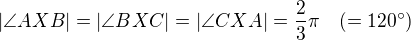Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 09. 2008 12:43
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Důkaz v trojúhelníku
Už je to delší čas, co jsem narazil na zajímavou úlohu, teď jsem si na ni vzpomněl v souvislosti se zahradou a kabelem:
Máme obecný trojúhelník ABC a bod X takový, že |AX|+|BX|+|CX| je minimální. Dokažte, že
Doufám, že si to pamatuji správně a jde to dokázat. Sám jsem to zatím nevyřešil, tak doufám, že jsem něco nepřehlédl a není to triviální :-)
Offline
#2 14. 09. 2008 14:30 — Editoval Marian (14. 09. 2008 14:38)
Re: Důkaz v trojúhelníku
Offline
#3 14. 09. 2008 14:38
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Důkaz v trojúhelníku
↑ Marian: Součet vzdáleností od vrcholů je opravdu* realizován v bodě, z nějž je všechny strany vidět pod úhlem 120˚. Je to celkem triviální důsledek Ptolemayovy věty a trojúhelníkové nerovnosti (i když je netriviální přijít na to, že se zrovna zde Ptolemayova věta uživí).
---
* pokud má trojúhelník všechny úhly menší než 120˚
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 14. 09. 2008 14:42
Re: Důkaz v trojúhelníku
↑ Kondr:
Nejprve jsem se přehlídnul a místo rovnítka mezi úhly měl za to, že ta jsou znaménka + pro jejich součet. Příspěvek jsem smazal a odkázal hned na materiály k Fermatově bodu.
Ptolemaiovu větu beru také jako možný prostředek.
Offline
#5 14. 09. 2008 14:51
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Důkaz v trojúhelníku
↑ Marian:
Aha, nevěděl jsem, že je to tak známá úloha. Díky za odkaz.
Takže co jsem napsal neplatí, platí to pouze pro trojúhelníky v nichž jsou všechny úhly menší než 120°.
Offline