Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 09. 2008 21:31 — Editoval jezza (13. 09. 2008 21:36)
Zahrada a kabel
Ahoj prosim vas všechny co mate bujnou matematickou představivost o pomoc s touto ulohou:
Je zahrada ve tvaru čtverce a stranách 100x100 metrů. Touto zahradou procházi kabel,u kterého nevime kudy procházi, ani jak velky kus toho kabelu prochází tou zahradou a který je rovně (prostě se nikam nezahýbá). mame zjistit kolik metru musíme vykopat, abychom ho našli a okopali co nejméně metrů zahrady.
můj vysledek ke kterému jsem se zatím dobádal je 270,71 m a prý je to moc a mam hledat dal. nákres tohoto řešeni je tadyhttp://forum.matweb.cz/upload/411-Obrázek1.jpg
díky moc za pomoc při vyrešení
Offline
#2 14. 09. 2008 01:35 — Editoval halogan (14. 09. 2008 11:30)
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Zahrada a kabel
Nejak nechapu zadani. Hlavne tu delku, smer a velikost.
Jestli vime, ze prochazi tou zahradou (tedy nekonci nekde v zahrade), tak staci okopat podel okraje. Ale to opravdu asi nechapu.
Edit: Uz to chapu tak, ze prochazi zahradou a nekonci slepe.
Offline
#3 14. 09. 2008 10:39
Re: Zahrada a kabel
Nojo, ale podel okraje je treba kopat 400m, reseni uvedene v prispevku vystaci se 270 metry kopani. Vcera vecer jsem nad tim premyslel, a fakt nemuzu prijit na zadne lepsi reseni. Zatim opravdu nemam tuseni, z jakeho konce na to jit, ono geometrie nikdy nebyla moje silna stranka, ale kdyby nekdo prisel na lepsi reseni, hrozne by me zajimalo jak vypada a jak na nej prisel, popripade dukaz, ze uz lepsi neexistuje by me taky hrozne zajimal.
Mam takove tuseni, ze ten ukol asi nebude prakticky (tedy ze nejde o to, skutecne potom vzit lopatu a kopat). Prece jenom zahrada 100x100 ma prilis idelani rozmery. Zajimalo by me, v souvislosti s jakou oblasti matematiky byla tahle uloha zadana, popripade jake znalosti se ocekavaji od jejiho resitele.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#4 14. 09. 2008 11:42 — Editoval BrozekP (15. 09. 2008 21:33)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zahrada a kabel
↑ jezza:
Malou změnou tvého řešení se dá dosáhnou kratší délky
Bod E leží na úsečce BD a 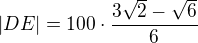 . Hledal jsem minimum vzdálenosti jako funkce |DE|. Takhle musíme vykopat
. Hledal jsem minimum vzdálenosti jako funkce |DE|. Takhle musíme vykopat 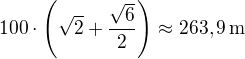 .
.
Offline
#5 14. 09. 2008 16:44
Re: Zahrada a kabel
↑ BrozekP:
a mužu se zeptat jak si na /DE/ přišel ? nebo co to je za delku?
Offline
#6 14. 09. 2008 18:28
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zahrada a kabel
↑ jezza:
To řešení co jsi uvedl ty je vlastně to moje, pokud bod E bude shodný s bodem D. Mě napadlo, že bych bod E posunul trochu k bodu B. Nevěděl jsem ale o kolik, tak jsem si vyjádřil celkovou délku co musíme kopat jako funkci vzdálenosti |ED|. Tuto funkci jsem zderivoval a našel minimum.
Offline
#7 14. 09. 2008 20:08
Re: Zahrada a kabel
↑ BrozekP:
Aha zderivoval.... to se budu učit asi tak za mesic tak proto jsem nevedel co to je... jo ale diky
Offline
#9 14. 09. 2008 22:54 — Editoval Marian (14. 09. 2008 22:59)
Re: Zahrada a kabel
↑ BrozekP:
Zkusil jsem jiný přístup a zkontroloval tak výpočet od BrozekP. Totiž pokud umístíme čtverec (stačí uvážit jednotkový) ABCD do kartezksého souřadnicového systému tak, že A=[0,0], B=[1,0], C=[1,1] a D=[0,1], pak je jasné, že bod E musí být (prvním) Fermatovým bodem trojúhelníka ACD. Jeho konstrukce je v tomto případě velice jednoduchá a jeho souřadnice spočte i dobrý žák osmé třídy klasické ZŠ. Dostaneme ![kopírovat do textarea $E=\left [\frac{1}{2}-\frac{\sqrt{3}}{6},\frac{1}{2}+\frac{\sqrt{3}}{6}\right ]$](/mathtex/07/077d5a7004b8f5105ee641a9e4edd8b4.gif) . Odtud se ona délka vykopaného příkopu spočte triviálně Pythagorovou větou.
. Odtud se ona délka vykopaného příkopu spočte triviálně Pythagorovou větou.
Tedy není třeba derivací, na druhou stranu se ale požaduje znalost Fermatova bodu, který jsme tady dneska shodou okolností probírali. Existují dokonce i zobecnění Fermatova bodu pro čtyřúhelníky. Možná by toto byla reálná alternativa pro řešení zadané úlohy. Je také ale docela možné, že řešení, jež navrhuje BrozekP bude lepší než pomocí zmiňovaného zobecnění. A to už vůbec nehovořím o optimální variantě.
Offline
#10 14. 09. 2008 23:42 — Editoval BrozekP (15. 09. 2008 00:49)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zahrada a kabel
Marian napsal(a):
Existují dokonce i zobecnění Fermatova bodu pro čtyřúhelníky. Možná by toto byla reálná alternativa pro řešení zadané úlohy.
Hledal jsem na internetu jak se určí Fermatův bod (jinak také Torricelliho bod) pro čtyřúhelník a podle toho co jsem našel je tímto bodem pro konvexní čtyřúhelník průsečík úhlopříček. Takže pro náš čtverec to jistě není řešení.
Díky tomu je ale zřejmé, že správný příkop nebude spojovat všechny rohy zahrady. (EDIT: moje chyba, není to zřejmé, zřejmé je pouze to, že správný příkop nevypadá jako čtyři úsečky z rohů do jednoho bodu někde uvnitř)
Offline
#11 15. 09. 2008 00:36
Re: Zahrada a kabel
Ted mi neni uplne jasne, z ceho to ma byti zrejme, ale pravdou je, ze existuje utvar, ktery spojuje vsechny ctyri rohy ctverce, a ktery ma (mysleno v souctu vsech casti) kratsi delku nez dve uhlopricky a navic vyhovuje zadani prikladu. Vypada takto:
\ /
\ /
\______/
/ \
/ \
/ \
Delka je asi 273 m (reseno hledanim minima funkce 4x + y, dvou promennych 'x', 'y', kde 'x' je delka jedne ze ctyr lomitkovych casti a 'y' je delka horizontalni usecky uprostred. Minimum samozrejme hledame na mnozine, jejiz body vyhovuji podmince, kladene na tvar toho obrazce. Ja jsem pri hledani minima pouzil Lagrangeovy neurcite koeficienty.)
Nekde jsem cetl, ze toto ma byt optimalni zpusob, jak propojit rohy obdelnika, nicmene uz si nemuzu vzpomnout, kde to presne bylo. Presto je toto reseni porad delsi nez to vubec prvni tady prezentovane. Z toho uz by melo plynout, ze je treba hledat utvar, jenz nespojuje vsechny ctyry rohy.
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#12 15. 09. 2008 08:39 — Editoval Cheop (17. 09. 2008 07:15)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Zahrada a kabel
Zahrada a kabel:
Pro lepší počítání budeme uvažovat, že čtvercová zahrada má jednotkové rozměry (z = 1)
Pak dle obrázku platí:
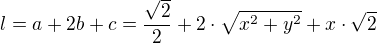
Dále platí: 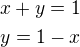
Nyní určíme délky x,y tak, aby výraz 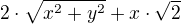 byl minimální pak:
byl minimální pak: 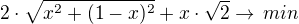 funkci zderivujeme a položíme rovnu 0
funkci zderivujeme a položíme rovnu 0 - úpravou
- úpravou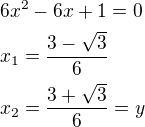 výsledek dosadíme do původní rovnice a dostaneme:
výsledek dosadíme do původní rovnice a dostaneme: +
+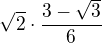 - úpravou:
- úpravou: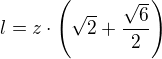 dosadíme-li za
dosadíme-li za 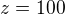 dostaneme
dostaneme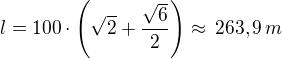
PS: Je to zřejmě úplně stejný výpočet, který tady prezentoval BrozekP, čímž ho zdravím.
Nikdo není dokonalý
Offline
#13 15. 09. 2008 09:11 — Editoval Marian (15. 09. 2008 10:16)
Re: Zahrada a kabel
↑ Lishaak:
Není třeba Langrangeovy multiplikátory. Počítal jsem onu "obálku" dneska v noci a měl jsem to za 5 minut pomocí Pythagorovy věty a extrémů funkce jedné proměnné. Obálka se tady už někde na fóru vyskytla, bohužel jsem ji nenašel. Výsledek máš ale správně.
Offline
#14 15. 09. 2008 10:30
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Zahrada a kabel
↑ Marian:↑ Cheop:Pokud známe topologické uspořádání výkopu, pak jeho optimální tvar získáme snadno když nad stranami čtverce sestrojíme rovnostranné trojúhelníky, nově vyniklé vrcholy s něčím* spojíme a použijeme Ptolemaiovu větu a trojúhelníkovou nerovnost k dukazu toho, že bod, v nemz se vykop rozdvojuje lezi na teto spojnici a na kruznici opsane nekteremu trojuhelniku. Ani v jednom případě není potřeba nic počítat. Problém je spíš ukázat, že dané uspořádání je nejlepší.
---
*V případě obálky spojujeme vrcholy trojúhelníků nad protějšími stranami. V případě (nejspíš) optimálního řešení spojujeme vrchol čtverce A s vrcholem trojúhelníka nad CD.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#15 15. 09. 2008 11:07 — Editoval Cheop (15. 09. 2008 11:27)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Zahrada a kabel
↑ Kondr:
Jen mě napadá taková praktická věc.
Pokud budeme kopat podél dvou stran na sebe kolmých a potom polovinu úhlopříčky, pak rozdíl mezi délkou kopání
v tomto případě a mnou a BrozkemP vypočítanou "optimální" délkou bude:![kopírovat do textarea $0,06815\cdot z\,[m]$](/mathtex/16/16180c070c300069277cd521090dea8a.gif) , kde
, kde  je strana zahrady,bude rozdíl zanedbatelný a nemusíme při tom dost složitě hledat bod E (BrozekP). Nepředpokládám zahradu větší jak 300 x 300 m (Při těchto rozměrech je rozdíl v kopání cca 20,5 metru). Dále jsem neviděl zahradu, která by měla přesný tvar čtverce, ale to už je jiná úloha.
je strana zahrady,bude rozdíl zanedbatelný a nemusíme při tom dost složitě hledat bod E (BrozekP). Nepředpokládám zahradu větší jak 300 x 300 m (Při těchto rozměrech je rozdíl v kopání cca 20,5 metru). Dále jsem neviděl zahradu, která by měla přesný tvar čtverce, ale to už je jiná úloha.
Nikdo není dokonalý
Offline
#16 15. 09. 2008 12:05
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zahrada a kabel
↑ Cheop:
Myslím, že praktická stránka nás tu příliš netrápí. Kdo má zahradu 100x100 metrů a hledá na ní přímý kabel, o jehož poloze nic neví :-)?
Já jsem třeba hledal i tak nepraktická řešení, že bych třeba kopal v každém bodě, který má racionální souřadnice. Míra množiny vykopaných bodů by pak byla nulová, takže bychom v podstatě nekopali vůbec :-) Bohužel to ale není řešení, jsou přímky, které neprocházejí žádným bodem, který má obě souřadnice racionální :-(
Offline
#17 15. 09. 2008 12:17
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Zahrada a kabel
↑ BrozekP:
Ale jistě, já to jako teoretický příklad bral.
Ještě jednou zdravím.
Nikdo není dokonalý
Offline
#18 15. 09. 2008 13:13
Re: Zahrada a kabel
BrozekP napsal(a):
jsou přímky, které neprocházejí žádným bodem, který má obě souřadnice racionální
Hm, tomuhle si mi nejak nechce verit...
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#19 15. 09. 2008 15:08
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zahrada a kabel
↑ Lishaak:
Co třeba přímka 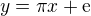 . Pokud je x racionální, pak y je iracionální, tedy neexistuje bod na přímce, který by měl obě souřadnice racionální.
. Pokud je x racionální, pak y je iracionální, tedy neexistuje bod na přímce, který by měl obě souřadnice racionální.
Offline
#20 15. 09. 2008 15:26 — Editoval Marian (15. 09. 2008 15:51)
Re: Zahrada a kabel
↑ BrozekP:
Zvol třeba x=1. Odkud víš, že pi+e je iracionální? Je to stále otvřený problém. Viz třeba zde (mezi vzorcem (6) a (7)).
To je věc lineární závislosti nebo nezávislosti reálných čísel. Ale mohl bys vzít třeba rovnici přímky 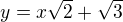 .
.
Offline
#22 15. 09. 2008 15:48 — Editoval Marian (15. 09. 2008 15:49)
Re: Zahrada a kabel
↑ Cheop:
To samozřejmě známo je, že tato dvě čísla jsou iracionální. Dokonce se už dosti dlouho ví, že tato dvě čísla nejsou algebraická nad tělesem Q. Tedy jinak řečeno, jsou to čísla transcendentní. To ovšem nestačí k tomu, abychom tvrdili, že číslo 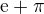 je iracionální (viz dokaz výše).
je iracionální (viz dokaz výše).
Offline
#23 15. 09. 2008 16:14 — Editoval BrozekP (15. 09. 2008 17:06)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Zahrada a kabel
↑ Marian:
Máš pravdu. Když jsem to psal tak jsem měl pocit, že jsem někde četl, že poměr pi/e není racionální číslo (edit: z čehož asi ani neplyne, že pi+e je iracionální), ten pocit byl špatný. Pokusím se příště vyvarovat podobných nepodložených tvrzení.
Offline
 tak
tak  ,jako základ přirozeného logaritmu, jsou obě dvě čísla iracionální
,jako základ přirozeného logaritmu, jsou obě dvě čísla iracionální