Matematické Fórum

Newbie · 13. 01. 2012 11:16 — Editoval Newbie (13. 01. 2012 11:18)

Ahoj, potřebuji poradit s problematikou zobrazení. Mám takový příklad a nevím řešení a nevím proč tomu tak je. Definice znám, ale zde to nedokážu využít.

Díky za rady a připomínky :)

EDIT: ještě mám menší dotaz... co znamená v matematice znak := ? díky

Aquabellla

↑ Newbie:

Injektivní = prosté zobrazení - buď je jenom rostoucí, nebo jenom klesající. (př: 2. obr. není prostý - nejdříve klesá, pak roste a pak zase klesá)
Surjektivní = zobrazení na - je využit celý obor hodnot (ze zadání všechna reálná čísla). Nenajdeš hodnotu na ose y, která by neměla vzor. (př: 1. obr není na - nemá hodnotu na 0.75)
Bijektivní - musí být zároveň prosté a zároveň na (kombinace předchozích dvou).

EDIT: znak := znamená přiřaď (je to z programování).

Například: a := 2 (do a přiřadím hodnotu dva, tudíž určuji, co daná proměnný symbolizuje za hodnotu).

Newbie · 13. 01. 2012 11:27 — Editoval Newbie (13. 01. 2012 11:33)

děkuji za odpověď, bohužel z tvé odpovědi mi není jasné jak je to s jednotlivými funkcemi.

1. obr ... surjektivní?
2. obr ... injektivní?
3. obr ... nvm

díky

Aquabellla · 13. 01. 2012 11:33

↑ Newbie:

1. obr: je injektivní (rostoucí na celém Df), ale není surjektivní (nemá hodnoty v tom "odskoku"), takže zobrazení není bijektivní.
2. obr: je surjektivní, obor hodnot je kompletní $H_f = R = (-\infty; +\infty)$ , ale není injektivní, tudíž není ani bijektivní.
3. obr: je injektivní (klesající na celém Df) a je surjektivní (nula je dodefinovaná tím puntíkem uprostřed), nabývá všech hodnot. Takže toto zobrazení je bijektivní.

Newbie · 13. 01. 2012 11:39 — Editoval Newbie (13. 01. 2012 11:43)

Ok,díky moc. Nyní už je mi to jasné. Rád bych se ještě zeptal na 2 zkouškové příklady.

"Napište co znamená, že funkce f je prostá na intervalu I."

a

"Napište dva polynomy p1(x) a p2(x) tak, aby p1(x) byla funkce v R prostá a p2(x) ne.

Díky moc! :)

Aquabellla · 13. 01. 2012 11:48

↑ Newbie:

Nejlepší je se naučit ty definice.

Funkce f je prostá na I, pokud pro všechna $x_1$ , $x_2$ z intervalu I platí: $f(x_1) = f(x_2) \Rightarrow x_1 = x_2$

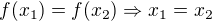
Příklad 2: polynom, který je prostý na celém Df, je například jakákoliv lineární funkce. Naopak kvadratická funkce (parabola) prostá není.

Newbie · 13. 01. 2012 11:52 — Editoval Newbie (13. 01. 2012 12:00)

Ok, díky.

p1(x)=2x+7
p2(x)=x^2 + 3x - 7

Takhle ten druhý příklad?

EDIT:

Mám tu definici injektivní funkce "Zobrazení f: A->B nazýváme injektivní (neboli prosté), jestliže pro každou dvojici x, y náleží Df, x se nerovná y, platí f(x) se nerovná f(y)". Ta definice platí i takhle že ? "Zobrazení f: A->B nazýváme injektivní (neboli prosté), jestliže pro každou dvojici x, y náleží Df, x se rovná y, platí f(x) se rovná f(y)".

Děkuji.

Aquabellla · 13. 01. 2012 12:05

↑ Newbie:

Ano, příklady máš správně.

Pozor, nemůžeš to jen tak vyměnit. Tyto dvě definice jsou ekvivalentní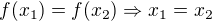
$f(x_1) = f(x_2) \Rightarrow x_1 = x_2$ ,
$x_1 \neq x_2 \Rightarrow f(x_1) \neq f(x_2)$
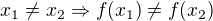
protože jde o "obměnu implikaci". Implikační znaménko je v definicích důležité.

Newbie · 13. 01. 2012 12:08

Aha, ok, už je mi to jasné. Tak moc děkuji, velice jsi mi pomohla.

Matematické Fórum

#1 13. 01. 2012 11:16 — Editoval Newbie (13. 01. 2012 11:18)

Zobrazení

#2 13. 01. 2012 11:21 — Editoval Aquabellla (13. 01. 2012 11:23)

Re: Zobrazení

#3 13. 01. 2012 11:27 — Editoval Newbie (13. 01. 2012 11:33)

Re: Zobrazení

#4 13. 01. 2012 11:33

Re: Zobrazení

#5 13. 01. 2012 11:39 — Editoval Newbie (13. 01. 2012 11:43)

Re: Zobrazení

#6 13. 01. 2012 11:48

Re: Zobrazení

#7 13. 01. 2012 11:52 — Editoval Newbie (13. 01. 2012 12:00)

Re: Zobrazení

#8 13. 01. 2012 12:00 Příspěvek uživatele Newbie byl skryt uživatelem Newbie. Důvod: hloupost

#9 13. 01. 2012 12:05

Re: Zobrazení

#10 13. 01. 2012 12:08

Re: Zobrazení

Zápatí