Matematické Fórum

mufik · 06. 01. 2012 21:29

Když zkrátíme matematické kyvadlo o 1/5 jeho délky zvětší se frekvence o 1/25Hz. Jak dlouhé bylo původně? (2,16m) děkuji za radu :-)

o.neill · 06. 01. 2012 21:42

Vztah pro výpočet frekvence matematického kyvadla je $f=\frac{1}{2\pi}\sqrt{\frac{l}{g}}$

Zamysli se nad tím, kolikrát se zvětší frekvence, když délku zkrátíme o pětinu.

mufik · 06. 01. 2012 22:22

↑ o.neill:
V tomto případě ze zadání se zvětší o 1/25Hz když to zkrátím o 1/5, tudíž to nové bude mít délku 4/5l ... ale bohužel nevím co s tím dál...

o.neill · 07. 01. 2012 13:13

Já se ptal kolikrát, ne o kolik. Kolikrát zjistíš z té rovnice ne ze zadání.

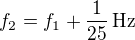Protože teď jedu pryč, poradím ti ještě další krok. Dejme tomu, že jsi zjistila, že se frekvence zdvojnásobí (což není pravda), pak $f_2=2f_1$ , zároveň ze zadání víš, že $f_2=f_1+\frac{1}{25}\,{\rm Hz}$ , máš tedy dvě rovnice o dvou neznámých.

mufik · 07. 01. 2012 14:15 — Editoval mufik (07. 01. 2012 14:28)

↑ o.neill:
tak abych zjistila f2 tak jsem si dala do poměru f1/f2, kde v f2 jsem za l dosazovala 4/5l (což by měla bý a nová délka) a zjistila jsem že f2=1,12f1, to jsem dala do té rovnice a f1 mi vyšlo 0,333Hz, pak jsem to dala do základního vztahu, ale to už mi pak nevychází

hfungus · 08. 01. 2012 15:29

kyvadlo (hmotnost M, délka závěsu L) je v aute, to jede v kruhu (polomer R) konst. rychlostí V. Jaká je frekvence kmitání kyvadla???? prosíííím. jaká?

hfungus · 09. 01. 2012 13:12

vyřešeno: $\omega =\frac{1}{2\pi }\sqrt{\frac{\sqrt{(\frac{v^{2}}{R})^{2}+g^{2}}}{L}}$

o.neill · 13. 01. 2012 21:50

Máš to dobře, já jsem ti napsal špatně vztah, je tam $\sqrt{\frac{g}{l}}$ za to se ti omlouvám, snad to teď už vyjde.

Matematické Fórum

#1 06. 01. 2012 21:29

matematické kyvadlo

#2 06. 01. 2012 21:42

Re: matematické kyvadlo

#3 06. 01. 2012 22:22

Re: matematické kyvadlo

#4 07. 01. 2012 13:13

Re: matematické kyvadlo

#5 07. 01. 2012 14:15 — Editoval mufik (07. 01. 2012 14:28)

Re: matematické kyvadlo

#6 08. 01. 2012 15:29

Re: matematické kyvadlo

#7 09. 01. 2012 13:12

Re: matematické kyvadlo

#8 13. 01. 2012 21:50

Re: matematické kyvadlo

Zápatí