Matematické Fórum

janina.kucera · 13. 01. 2012 23:20

Ahoj,
potřebovala bych prosím poradit s jedním příkladem. Mám dokázet, že 7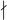 $\nmid$ a $^{3}$ + b $^{3}$ - 3.
Děkuju moc

vanok · 13. 01. 2012 23:25

Ahoj ↑ janina.kucera:,
Prva myslienka
urobit tabulku zo vstupmy a ; b modulo 7
cize bude tam 49 vysledkov na doplnenie
a konstatujes ci tam budu 0 (nuly) modulo 7

Ak nikde tam nebude 0, tak take cislo nie je nikdy delitelne 7mimy

Ak mi napadne nieco ine napisem.

janina.kucera · 13. 01. 2012 23:25

↑ janina.kucera:
Přepsala jsem výraz: $7\nmid a^{3}+b^{3}-3$

janina.kucera · 13. 01. 2012 23:30

↑ janina.kucera:
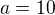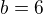Nějak takto jsme to dělala. Vlastně když mám, že $a=10$ a $b=6$ , tak mi vyjdou zbytky 6 a 6. Takže potom do tabulky napíšu 12, nebo od toho ještě odečtu 3.

janina.kucera · 13. 01. 2012 23:34

↑ janina.kucera: a se mělo rovnat 5 a b se rovná 6

vanok · 13. 01. 2012 23:38

↑ janina.kucera:,
Druha metoda:
A zda sa mi pekna

Urobil som tabulku cisiel 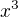$x^3$ pre vsetky cisla modulo 7

UROB JU

napr. 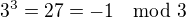$3^3=27=-1\mod 3$

A som konstatoval v tabulke ze su vsetky -1; 0, alebo 1 modulo 7

Sucet takych dvoch cisiel $a^3+ b^3$ moze mat hodnoty -2;-1;0; 1 alebo 2 mod 7
a ak odcitame 3 modulo 7
cize hodnoty $a^3+ b^3-3$ mozu byt -5;-4;-3;-2 alebo -1 modulo 7
Akoze v tomto zozname nie je 0 (mod 7) ziadne z cisiel $a^3+ b^3$ nemoze byt delitelne 7mimy.

janina.kucera · 13. 01. 2012 23:50

↑ vanok:
Více se mi líbila ta první myšlenka, i když je to vlastně skoro to samé, ale ted ještě řeším problém, že je nemožné to dokazovat pro všechna čísla do $\infty$ , stačilo by to dokázat jen pro interval od 0 do 6, ale když buud mít např. a=10, jak toto $7/10^{3}+6^{3}-3 \Leftrightarrow 7/3^{3}+6^{3}-3$ napíšu obecně?

vanok · 14. 01. 2012 00:14

↑ janina.kucera:,
Aritmetika modulo 7, je taka co sa zaobera len zbytkamy delennim 7mimy.
Cize tabulka nasobenia a scitania sa podoba na tu o ktorej pisem v prvej metode

Ta druha, pouziva uz nejake matematicke uvahy... a vdaka tomu sa nemusia ani robit tabulky...

No to zalezi na tebe co si vyberes.
Uvahy sa pacia profesorom....
a tabulkam sa lahsie rozumie

TAK POSUD A VYBER CO MYSLIS!

A mozno najdes aj tretiu metodu?????

janina.kucera · 14. 01. 2012 00:22

↑ vanok:děkuju, moc jsi mi pomohl :)

Matematické Fórum

#1 13. 01. 2012 23:20

Důkaz, že výraz není dělitelný 7

#2 13. 01. 2012 23:25

Re: Důkaz, že výraz není dělitelný 7

#3 13. 01. 2012 23:25

Re: Důkaz, že výraz není dělitelný 7

#4 13. 01. 2012 23:30

Re: Důkaz, že výraz není dělitelný 7

#5 13. 01. 2012 23:34

Re: Důkaz, že výraz není dělitelný 7

#6 13. 01. 2012 23:38

Re: Důkaz, že výraz není dělitelný 7

#7 13. 01. 2012 23:50

Re: Důkaz, že výraz není dělitelný 7

#8 14. 01. 2012 00:14

Re: Důkaz, že výraz není dělitelný 7

#9 14. 01. 2012 00:22

Re: Důkaz, že výraz není dělitelný 7

Zápatí