Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 01. 2012 22:50
tecna a normalna slozka zrychleni
Urcete drahu pohybu daneho rovnicemi x1 = 3+4cost , x2=2+5sint , jeho rychlost, zrychleni , tecnou a normalovou slozku zrychleni. Vsechno mam spocitane, akorat jsem se zasekl u toho tecneho a normaloveho zrychleni. Problem je, ze nemuzu pouzit an=v^2/R a at=dv/dt. Jak na to?
Offline
- (téma jako vyřešené označil(a) SoniCorr)
#3 14. 01. 2012 09:27
Re: tecna a normalna slozka zrychleni
↑ SoniCorr:
rychlost dostaneš zderivováním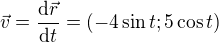
dalčí derivace dává zrychlení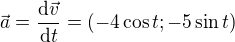
Nyní trocha geometrie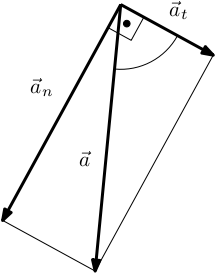
měl bys vidět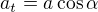
pro odchylku dvou vektorů 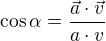 (protože
(protože  a
a  leží na stejné přímce)
leží na stejné přímce)
takže 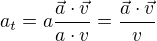
dosadíme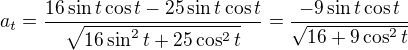 (bereš v absolutní hodnotě - je to velikost)
(bereš v absolutní hodnotě - je to velikost)
Normálovou složku spočítáme z Pythagorovy věty ( vůbec nepotřebuješ)
vůbec nepotřebuješ)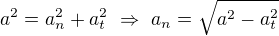
tam si dosaď a spočítej si sám.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
