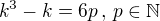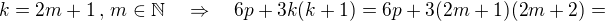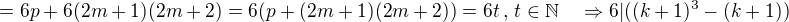Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz matematickou indukcí (TOTO TÉMA JE VYŘEŠENÉ)
#1 15. 01. 2012 14:12
Důkaz matematickou indukcí
Zadání:
Dokažte matematickou indukcí, že číslo 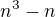 je dělitelné 6ti, pro každě přirozené n.
je dělitelné 6ti, pro každě přirozené n.
Řešení:
pro každé přirozené číslo n => n>0
číslo je dělitelné 6ti, právě tehdy, když je dělitelné 2mi a 3ma zároveň
Indukční základ:


Indukční základ platí
Indukční krok: 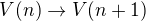
Indukční předpoklad: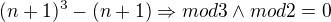
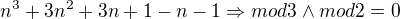
![kopírovat do textarea $[(n^{3}-n)+(3n^{2}+3n)]\Rightarrow mod3\wedge mod2=0$](/mathtex/bd/bdef24286b084794aa5ad7d0fb294828.gif)
Potřeboval bych prosím poradit jestli postupuju dobře, popřípadně jak postupovat dál, víc si nevím rady :(
Offline
- (téma jako vyřešené označil(a) Ryco)
#2 15. 01. 2012 18:39 — Editoval jardofpr (15. 01. 2012 18:40)
Re: Důkaz matematickou indukcí
↑ Ryco:
povedal by som, že to vidíš príliš komplikovane ..
zmysel dôkazu indukciou tvrdenia typu "dokážte pre všetky prirodzené n" alebo "pre všetky prirodzené n>=m" kde m je nejaké konkrétne prirodzené číslo je v tom, že
1.) dokážeš že výrok platí pre n=1 (v prípade že máš dolnú hranicu dokážeš že platí výrok pre n=m)
2.) z predpokladu že výrok platí pre prirodzené číslo k vyvodíš že platí aj pre o jedno väčšie, pričom
ten predpoklad je pri tom často veľmi užitočný
tým máš platnosť výroku dokázanú pre všetky n ktoré spĺňajú zadanie, lebo keď si zvolíš ľubovoľné n prirodzené,
z 1.) vieš že pre najmenšie to platí a z 2.) vieš že to platí pre o jedno väčšie, ale potom to zasa platí pre o jedno väčšie, atď až sa dostaneš k ľubovoľnému n prirodzenému ...
takže tebe stačí:
1.)ukázať že to platí pre n=1
2.)indukčný krok:
dokázať ,že z toho že pre n=k výrok platí ukázať že platí aj pre n=k+1
skús pokiaľ sa dostaneš
Offline
#3 15. 01. 2012 21:33 — Editoval Ryco (16. 01. 2012 11:20)
Re: Důkaz matematickou indukcí
Řešení:
pro každé přirozené číslo n => n>0
číslo je dělitelné 6ti, právě tehdy, když je dělitelné 2mi a 3ma zároveň
Indukční základ:
Indukční základ platí
Indukční krok: 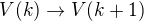
Indukční předpoklad: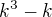
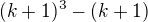
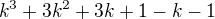
![kopírovat do textarea $[(k^{3}-k)+(3k^{2}+3k)]$](/mathtex/3d/3ded39afdca651cc9717505547c754b6.gif)
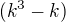 ..... je dělitelné 6ti viz Indukční Základ
..... je dělitelné 6ti viz Indukční Základ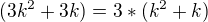
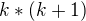 => I.P. platí?
=> I.P. platí?
Offline
#5 15. 01. 2012 22:00 — Editoval jardofpr (15. 01. 2012 22:00)
Re: Důkaz matematickou indukcí
↑ Ryco:
vieš, každého to učia písať inak mám taký pocit niekedy ..
dôležité je, aby bolo jasné ktorá časť je ktorá
ja som to zvykol rozlišovať ako číslo kroku
1.) n=1
dokazovanie pre n=1
2.) IP:pre n=k platí: 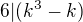
(pre náś prípad)
3.)pre n=k+1?
dokazovanie pre k+1
ale niekto ti povie že sú to len dva kroky a podobne, takže je to asi rôzne, hlavne aby sa v tom dalo vyznať a nebolo to matematicky nesprávne zapísané
Offline
#7 16. 01. 2012 00:40
Re: Důkaz matematickou indukcí
↑ Ryco:
nie, keď chceš niečo dokázať pre nejakú skupinu čísel, nestačí že si jedno vyberieš, čo tie ostatné potom?
chceš ukázať že 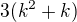 je deliteľné šiestimi, teda už potrebuješ iba to že
je deliteľné šiestimi, teda už potrebuješ iba to že 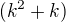 je deliteľné dvomi
je deliteľné dvomi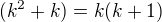 je súčin dvoch po sebe idúcich prirodzených čísel a keďže sa striedajú štýlom párne, nepárne, párne, nepárne,...
je súčin dvoch po sebe idúcich prirodzených čísel a keďže sa striedajú štýlom párne, nepárne, párne, nepárne,...
jedno z nich je určite párne, a teda deliteľné dvomi ;-)
Offline
#8 16. 01. 2012 00:51 — Editoval Peggy1012 (16. 01. 2012 00:52)
Re: Důkaz matematickou indukcí
↑ Ryco:
Ahojda, já bych ještě využila toho, že číslo, které je dělitelné 2 je ve tvaru 2k, z toho 6 je ve tvaru 6k. Takže nejdřív dokážeme, že 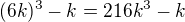 je dělitelné 6, to pak vezmeme jako indukční předpoklad.
je dělitelné 6, to pak vezmeme jako indukční předpoklad.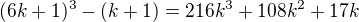 =
=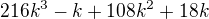
Je zřejmé, že je nejen indukční předpoklad, ale i "zbytek" je dělitelný 6.
Offline
#11 16. 01. 2012 11:38
Re: Důkaz matematickou indukcí
pochopil sem to tak že dělitelné 3mi je proto protože je před tou závorkou ta 3jka. A dále dělitelné 2mi protože když dosadím liché číslo tak to budé (liché * sudé)=sudé, a když dosadím číslo sudé tak to bude (sudé*liché)=sudé. Sudé je vždy dělitelné 2mi. tudiž platí že číslo je dělitelné 3ma a 2mi zároveň.
Offline
#13 16. 01. 2012 11:42
Re: Důkaz matematickou indukcí
↑ jardofpr:
ok, takže jak to teď do toho příkladu zapsat matematicky správně? stačí to udělat tak, že napíšu tu závorku ve tvaru 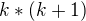 a napsat, že z toho vyplývá platnost indukčního předpokladu?
a napsat, že z toho vyplývá platnost indukčního předpokladu?
Offline
#15 16. 01. 2012 12:39
Re: Důkaz matematickou indukcí
↑ jardofpr:
aha ok, no todle vypadá hlavně o dost složitěji. Budu se spoléhat, že na písemce bude stačit tendle jednodušší postup =). Díky za pomoc
Offline
#17 16. 01. 2012 12:48
Re: Důkaz matematickou indukcí
↑ jardofpr:
jojo, stejne u zkousky tam musime mit k tomu postupu i nejaky slovni zapis, aby viděli, že tomu rozumíme. Takže by to mělo stačit. Ještě jednou dík. Téma označuju za vyřešené.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Důkaz matematickou indukcí (TOTO TÉMA JE VYŘEŠENÉ)