Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Tečna a normála přímka p (TOTO TÉMA JE VYŘEŠENÉ)
#1 20. 01. 2012 10:16
Tečna a normála přímka p
Ahoj,
vůbec si s tím nevím rady, poradíte mi někdo prosím s postupem?
Jaká musí být hodnota čísla q, aby přímka -8x+4y+q=0 byla tečnou grafu y=-x²+6x+1
Výsledek by měl být -20
a ještě pro normálu
Jaká musí být hodnota čísla q, aby přímka 2x+2y+q=0 byla normálou grafu y=2x²+9x-9
Výsledek by měl být 42
Díky moc.
B.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 20. 01. 2012 10:47
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Tečna a normála přímka p
↑ xducb100:
Ahoj, zkus si projít toto téma, řeší se tam to samé.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#3 20. 01. 2012 10:57
Re: Tečna a normála přímka p
↑ Aquabellla:
To jsem procházla, než jsem sem napsala. Ale podle toho, jak to počítám, tak dělám asi někde chybu a vůbec mi nevychází to, co by mělo.. A děkuji za pomoc..
Offline
#4 20. 01. 2012 11:12 — Editoval Honzc (20. 01. 2012 11:17)
Re: Tečna a normála přímka p
↑ xducb100:
ad1.
1. Tečna grafu (tady tečna paraboly) má tu vlastnost, že má s tou parabolou pouze jeden společný bod (bod dotyku).
2. Toho využijeme. Z rovnice tečny vyjádříš  . Mají-li se přímka s parabolou dotýkat, pak se v bodu dotyku rovnají i jejich y-ové souřadnice. Tedy položíš ypřímky = yparaboly.
. Mají-li se přímka s parabolou dotýkat, pak se v bodu dotyku rovnají i jejich y-ové souřadnice. Tedy položíš ypřímky = yparaboly.
Dostaneš kvadratickou rovnici. Aby přímka byla tečnou musí mít s parabolou pouze jeden společný bod. A teď otázka. Kdy má kvadratická rovnice pouze jedno řešení? No přece, když je diskriminant k.r. roven nule. Tak si napíšeš rovnici diskriminantu (ta bude obsahovat i neznámou  ) položíš ji rovnu nule. Vypočítáš
) položíš ji rovnu nule. Vypočítáš  a je hotovo.
a je hotovo.
2. Tady využiješ toho, že nejdříve napíšeš rovnici tečny (tečna má směrový vektor kolmý na směrový vektor normály). Praktické vyjádření. Máš-li zadánu nějakou přímku v obecném tvaru např.  , pak přímka kolmá na tuto přímku má obecnou rovnici bx-ay+d=0
, pak přímka kolmá na tuto přímku má obecnou rovnici bx-ay+d=0
Toho tedy využiješ, napíšeš si obecnou rovnici tečny, (a zase stejně jako u př. 1) dosadíš a dostaneš kvadratickou rovnici. Z té spočítáš x-ovou souřadnici bodu dotyku (s výpočten diskriminantu se nemusíš počítet, neboť bude 0). Tuto vypočtenou x-ovou souřadnici dosadíš do rovnice paraboly a tak spočítáš y-ovou souřadnici bodu dotyku. Tento bod musí ležet i na normále (leží samozřejmě i na tečně-ale to nás nezajímá). Tak ho dosadíš do rovnice normály a z dané rovnice vypočítáš 
Offline
#5 20. 01. 2012 11:13 — Editoval Aquabellla (20. 01. 2012 11:14)
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Tečna a normála přímka p
↑ xducb100:
Tečna:  =>
=>  . Takže směrnice tečny je
. Takže směrnice tečny je  .
.
Derivace:  =>
=>  =>
=>  - toto je bod dotyku.
- toto je bod dotyku.
Teď stačí dosadit do rovnice  a po úpravě mi vyšlo, že q = 20.
a po úpravě mi vyšlo, že q = 20.
Už jsi našla chybu nebo mám to mám rozepsat dál? :-)
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#6 20. 01. 2012 11:16
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Tečna a normála přímka p
↑ xducb100: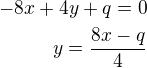 toto dosadíme do rovnice paraboly
toto dosadíme do rovnice paraboly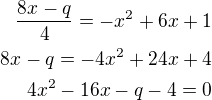 aby to byla tečna, potom diskriminant této kv. rovnice D=0 (tečna bude mít s parabolu 1 společný bod)
aby to byla tečna, potom diskriminant této kv. rovnice D=0 (tečna bude mít s parabolu 1 společný bod)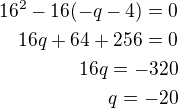
Máš vypočíráno
Nikdo není dokonalý
Offline
#9 20. 01. 2012 11:37
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Tečna a normála přímka p
Nechci se do toho vměšovat, jen poznamenám, že postup od ↑ Aquabellla: není sice tak universální jako ten od ↑ Cheop:, ale využívá vlastností těch funkcí a je více "vidět" ten výsledek, je přirozenější. Když si to navíc člověk nakreslí, tak je to perfektně vidět.
Nejlepší je samozřejmě znát oba postupy.
Offline
#11 20. 01. 2012 12:29
#12 20. 01. 2012 13:32
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Tečna a normála přímka p
↑ xducb100:
Př.2)
1)Normála nějaké křivky je přímka kolmá k tečně procházející tečným bodem
Normála má mít dle zadání rovnici: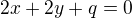
Tečna bude kolmá k této přímce a bude tečnou k parabole
Normálový vektor hledané tečny bude: 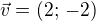
Rovnice tečny bude: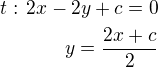 toto je rovnice tečny k uvedené paraboly
toto je rovnice tečny k uvedené paraboly
Vypočteme souřadnice tečného bodu: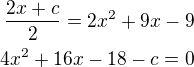 - diskriminant bude D=0(je to tečna) tedy:
- diskriminant bude D=0(je to tečna) tedy: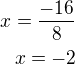 - x-ová souřadnice tečného bodu
- x-ová souřadnice tečného bodu
Dopočteme y-ovou souřadnici tečného bodu - dosadíme x-ovou souřadnici do rovnice paraboly 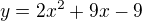 a dostaneme
a dostaneme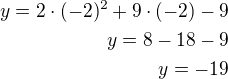
Souřadnice tečného bodu: 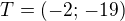
Normála bude procházet tečným bodem - dosadíme souřadnice tohoto bodu do rovnice 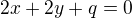 a dopočteme q
a dopočteme q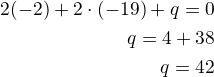
Rovnice normály: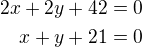
Nikdo není dokonalý
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Tečna a normála přímka p (TOTO TÉMA JE VYŘEŠENÉ)