Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 21. 01. 2012 15:30
Offline
#4 21. 01. 2012 16:24
Re: x
↑ xducb100:
Nechtělo by to sem dát přesné zadání?
Takhle se x může rovnat čemukoliv. (v závislodti od C)
Offline
#5 21. 01. 2012 16:54
Re: x
Tady jsou dva příklady, který jsou podobný tomu, co jsem sem dávala..Pod tím je i postup..
Jaká musí být hodnota čísla q, aby přímka -8x+4y+q=0 byla tečnou grafu y=-x²+6x+1
Výsledek by měl být -20
a ještě pro normálu
Jaká musí být hodnota čísla q, aby přímka 2x+2y+q=0 byla normálou grafu y=2x²+9x-9
Výsledek by měl být 42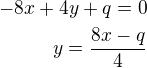
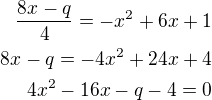
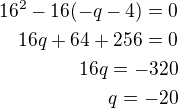
Všechno nějak tak vím, jak se počítá, ale nevím v tom 3. kroce ten první řádek
a potom: 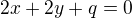
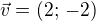
Rovnice tečny bude: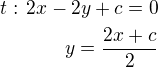
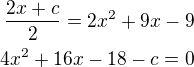
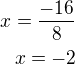 - x-ová souřadnice tečného bodu
- x-ová souřadnice tečného bodu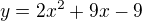 a dostaneme
a dostaneme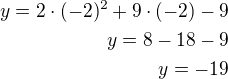
Souřadnice tečného bodu: 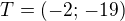
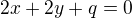 a dopočteme q
a dopočteme q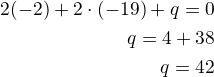
Rovnice normály: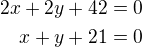
Tady zase nevím ten krok, jak se dostene z toho to x.
Moc děkuji za radu..
Offline
#6 21. 01. 2012 17:40
- janca361

- .
- Příspěvky: 3284
Re: x
↑ xducb100:
A to se učí na základní škole jo?
Založ si pro nový příklad nové téma v odpovídající sekci (SŠ?)
Offline

