Matematické Fórum

xducb100 · 21. 01. 2012 18:29

Ahoj, mohli by jste mi prosím poradit?

Jaká musí být hodnota čísla q, aby přímka -8x+4y+q=0 byla tečnou grafu y=-x²+6x+1
Výsledek by měl být -20

a ještě pro normálu

Jaká musí být hodnota čísla q, aby přímka 2x+2y+q=0 byla normálou grafu y=2x²+9x-9
Výsledek by měl být 42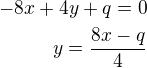

$-8x+4y+q=0\\y=\frac{8x-q}{4}$
$\frac{8x-q}{4}=-x^2+6x+1\\8x-q=-4x^2+24x+4\\4x^2-16x-q-4=0$
$16^2-16(-q-4)=0\\16q+64+256=0\\16q=-320\\q=-20$

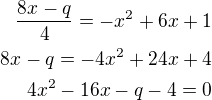
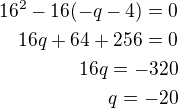
Všechno nějak tak vím, jak se počítá, ale nevím v tom 3. kroce ten první řádek

a potom: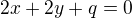

$2x+2y+q=0$
$\vec{v}=(2;\,-2)$

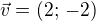
Rovnice tečny bude: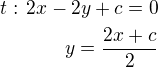
$t:\,2x-2y+c=0\\y=\frac{2x+c}{2}$

$\frac{2x+c}{2}=2x^2+9x-9\\4x^2+16x-18-c=0$
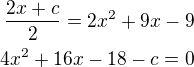
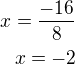$x=\frac{-16}{8}\\x=-2$ - x-ová souřadnice tečného bodu
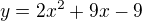$y=2x^2+9x-9$ a dostaneme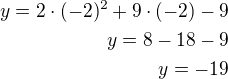
$y=2\cdot(-2)^2+9\cdot(-2)-9\\y=8-18-9\\y=-19$
Souřadnice tečného bodu: 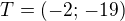$T=(-2;\,-19)$
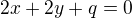$2x+2y+q=0$ a dopočteme q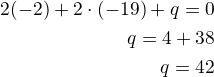
$2\xdot(-2)+2\cdot(-19)+q=0\\q=4+38\\q=42$
Rovnice normály: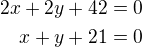
$2x+2y+42=0\\x+y+21=0$

Tady zase nevím ten krok, jak se dostene z toho to x.

Moc děkuji za radu..

jelena · 21. 01. 2012 21:21

Zdravím,

nepiš, prosím, různé úlohy do jednoho tématu je to nepřehledné - viz pravidla.

Všechno nějak tak vím, jak se počítá, ale nevím v tom 3. kroce ten první řádek

poslední krok "2. bloku" je kvadratická rovnice s parametrem q. Potřebuješ, aby tato rovnice měla pouze jeden (dvojnásobný) kořen, protože jen tak přímka a parabola mají jeden společný bod a přímka je tečnou. V 3. kroku jsi zapsala diskriminant 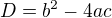$D=b^2-4ac$ a položila ho rovný nule. Dopočteš q.

-----------------------------------------------
Rovnice normály

Tady zase nevím ten krok, jak se dostene z toho to x

(pokud rovnice normály je 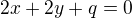$2x+2y+q=0$ , potom normálový vektor pro tečnu je 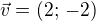$\vec{v}=(2;\,-2)$ ) a došla jsi k:
$\frac{2x+c}{2}=2x^2+9x-9\\4x^2+16x-18-c=0$ ,

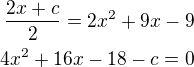zde jsi opět měla najít takové c, aby kvadratická rovnice měla jen jeden kořen (tedy přes D=0). Postupovala jsi také tak?

Potom stačilo c dosadit do rovnice tečny, najít průsečík tečny a paraboly - bod T(x, y). Tento bod zároveň náleží normále, proto dosadíme x, y do rovnice normály, najdeme q. Podaří se zorientovat? Děkuji.

xducb100 · 22. 01. 2012 10:41

↑ jelena: To první mi je už jasný a u toho druhýho nevím, jak přímo tu rovnici udělat, aby mi to x vyšlo -16/8 = -2, nevím, jak příjdu na to -16/8.. A ten vektor je vyloženě, že vezmu ty čísla z rovnice pro tečnu x a y nebo se to nějak počítá? Děkuji..

jelena · 22. 01. 2012 12:11

↑ xducb100:

Jelikož přispíváš do VŠ, tak předpokládám, že tuto úlohu řešíš na VŠ. Zopakuj si z analytické geometrie rovnice přímky v obecném tvaru. Rovnice tečny je v obecném tvaru, ze kterého vytáhneme normálový vektor. Tento vektor můžeme použit rovnou a bude směrový pro rovnici normály v parametrickém tvaru. Nebo tento vektor "promeníme" na kolmý - přehodíme souřadnice a změníme jedno znaménko. Tak vytvoříme normálový vektor pro obecnou rovnici nové přímky=normály ke grafu.

jak přímo tu rovnici udělat, aby mi to x vyšlo -16/8 = -2, nevím, jak příjdu na to -16/8.

To netuším. Postupovala bych přes výpočet parametru c z nulového D, potom bych c dosadila do rovnice tečny.

Cheop · 23. 01. 2012 07:23 — Editoval Cheop (23. 01. 2012 08:33)

↑ jelena:
Zdravím
protože tato rovnice 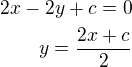$2x-2y+c=0\\y=\frac{2x+c}{2}$ má být rovnicí tečny k této parabole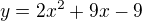 $y=2x^2+9x-9$
potom diskriminant této kvadratické rovnice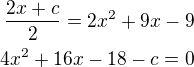 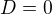$\frac{2x+c}{2}=2x^2+9x-9\\4x^2+16x-18-c=0$ $D=0$ čili
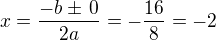$x=\frac{-b\pm\,0}{2a}=-\frac{16}{8}=-2$ parametr c tedy nemusíme počítat (nám nejde v tomto kroku o rovnici tečny, ale o souřadnice tečného bodu),
které budeme potřebovat na určení q této normály: 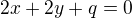$2x+2y+q=0$

A potom z této rovnice 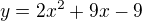$y=2x^2+9x-9$ dopočteme y-ovou souřadnici tečného bodu

A nakonec dosadíme do rovnice normály 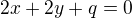$2x+2y+q=0$ souřadnice tečného bodu a dopočteme q

Honzc · 23. 01. 2012 07:57

↑ xducb100:
Čteš ty vůbec ty naše příspěvky? Nebo na nás kašleš? Za prvé jedno téma (příkaldy) píšeš pořád dokola někde jinde a za druhé jsem ti psal podrobně jak se to dělá a ↑ Cheop: ti to podle toho spočítal.

jelena · 23. 01. 2012 10:18

Zdravím vás,

↑ Cheop:

moc děkuji, to mi nedošlo, že stačí rovnou uvažovat D=0.

↑ Honzc:

kašle :-)

Je to i moje chyba - v sobotu večer jsem uklízela virtuální plácek a našla jsem kolegyňku s řešením - nekontrolovala jsem čísla a myslela jsem si, že počítá něco stejného, jen v jiných číslech. Jinak bych samozřejmě zametla a setřela.

Jinak, dej si někdy tu práci a sleduj efektivitu reakce na dotazy (to dělám :-) - kolik je zpětné odezvy od autorů dotazů. Také v rámci benchmarkingu občas se procházím po jiných fórech - stejné dotazy na více místech, tak proč by si dělali těžkou hlavu s odezvou.

---------------------------------

"Já proti tomu apriori nejsem, ale jsem apriori proti tomu, abych se o to staral já :-)" (c)

xducb100 · 23. 01. 2012 10:57

↑ Honzc: Čtu, ale s matematikou trochu válčím.. Začla jsem se ji učit pořádně teď na vysoký, protože na střední jsme měli učitele alkoholika, který neměl potřebu vyučovat látku, která se zrovna měla probírat.. Takže se ji učím teď od začátku.. Omlouvám se za zmatky.. Mrzí mě to..

Cheop · 23. 01. 2012 11:28

↑ xducb100:
Doufám, že ted už Ti je ten příklad jasný.
Omluva se přijímá.
Můžeš tedy příklad označit za vyřešený.

xducb100 · 23. 01. 2012 11:56

↑ Cheop: Jo, je děkuji.. Označím..

Matematické Fórum

#1 21. 01. 2012 18:29

Tečna a normála přímka p výraz x

#2 21. 01. 2012 21:21

Re: Tečna a normála přímka p výraz x

#3 22. 01. 2012 10:41

Re: Tečna a normála přímka p výraz x

#4 22. 01. 2012 12:11

Re: Tečna a normála přímka p výraz x

#5 23. 01. 2012 07:23 — Editoval Cheop (23. 01. 2012 08:33)

Re: Tečna a normála přímka p výraz x

#6 23. 01. 2012 07:57

Re: Tečna a normála přímka p výraz x

#7 23. 01. 2012 10:18

Re: Tečna a normála přímka p výraz x

#8 23. 01. 2012 10:57

Re: Tečna a normála přímka p výraz x

#9 23. 01. 2012 11:28

Re: Tečna a normála přímka p výraz x

#10 23. 01. 2012 11:56

Re: Tečna a normála přímka p výraz x

Zápatí