Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 11. 2007 16:12 — Editoval sneakfast (13. 11. 2007 22:51)
Vnořené intervaly
zdravím, mám takový celkem hloupý problém.. ve skriptech jsem nalezl větu, které nevěřím, potřeboval bych poradit s objasněním.
Věta: Jestliže pro uzavřené intervaly 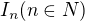 platí
platí  , pak
, pak 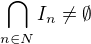 Jestliže navíc délky intervalů I_n klesají k nule, pak je tento průnik jednobodový.
Jestliže navíc délky intervalů I_n klesají k nule, pak je tento průnik jednobodový.
Podle mě nemůže být jednobodový, protože to je spor s definicí intervalu, ve kterém se podle skript, ze kterých čerpám, jako uzavřený interval bere <a, b> tak, že a < b .
diky za odpoved:)
Offline
#3 13. 11. 2007 23:01
Re: Vnořené intervaly
opraveno..
mě by bylo všechno jasné, kdyby definice intervalu připouštěla interval degenerovaný, potom bych i přes tu poměrně vágní formulaci "délky klesají k nule" neměl problém. Ale zajímalo by mě, jestli je možné tuto větu dokázat i bez degenerovaných intervalů, snad nějak limitně?
Offline
#4 13. 11. 2007 23:16
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Vnořené intervaly
 je množina, která obecně nemusí být intervalem, může mít pouze jeden prvek. (Zřejmě průnik konečně mnoha intervalů je interval, ale pokud děláme průnik přes nekonečnou množinu, tak to platit nemusí.)
je množina, která obecně nemusí být intervalem, může mít pouze jeden prvek. (Zřejmě průnik konečně mnoha intervalů je interval, ale pokud děláme průnik přes nekonečnou množinu, tak to platit nemusí.)
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 14. 11. 2007 00:11
Re: Vnořené intervaly
Mějme dva intervaly I_n, I_{n+1} tak, že platí I_{n+1} je podmnožinou I_n.
Průnikem intervalů I_n a I_{n+1} je interval I_{n+1}.
Je dána množina intervalů I_k; k = 1,2,3,...
Pro každé I_k platí: I_{k+1} je podmnožinou I_k.
Indukce:
Pokud I_k, I_{k+1} jsou intervaly, jejich průnikem je I_{k+1}, což je interval.
Pro I_1 a I_2 zjevně platí podle definice intervalu.
je tedy možné, že pro libovolné k platí výše uvedené, ale v limitě interval zdegeneruje?
nebo je i v této úvaze chyba?
Offline
#6 14. 11. 2007 01:21
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Vnořené intervaly
Tato úvaha korektně dokazuje to, o čem jsem psal:průnik konečně mnoha intervalů je interval.
Pro nekonečnou indexovou množinu to ale neplatí a pokud bychom si definovali limitu posloupnosti intervalů, pak by se v tomto případě stalo, že by nebyla intervalem, ale jednoprvkovou množinou.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#7 15. 11. 2007 14:03 — Editoval Marian (15. 11. 2007 14:05)
Re: Vnořené intervaly
Posledni sneakfastuv prispevek bych chtel dodatecne jeste doplnit. Kdyby bylo skutecne splneno, ze delky intervalu I_{n} by konvergovaly k nule pro  , pak bys mohl dokazat tvrzeni o degeneraci intervalu v izolovany bod napriklad sporem. Presneji myslim toto:
, pak bys mohl dokazat tvrzeni o degeneraci intervalu v izolovany bod napriklad sporem. Presneji myslim toto:
Necht delka intervalu 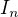 je oznacena
je oznacena 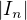 pro vsechna
pro vsechna 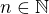 a
a 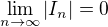 .
.
Predpokladejme sporem, ze mnozina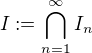 je intervalem, tedy existuje dvojice
je intervalem, tedy existuje dvojice  takova, ze
takova, ze ![kopírovat do textarea $I=[\alpha ,\beta]$](/mathtex/dd/ddd3f74951d72e941f28a11db2e4bde7.gif) ,
,  . Pak se da snadno ukazat, ze lze nalezt takove prirozene cislo
. Pak se da snadno ukazat, ze lze nalezt takove prirozene cislo  , ze pro vsechna
, ze pro vsechna 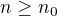 ,
, 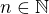 , plati
, plati![kopírovat do textarea $[\alpha ,\beta]\supset \bigcap_{k=1}^{n}I_k$](/mathtex/14/148bfed5ac994132433b8c66ffe60a0d.gif) , coz je jasny spor s predpokladem o tom, ze interval
, coz je jasny spor s predpokladem o tom, ze interval ![kopírovat do textarea $[\alpha ,\beta]$](/mathtex/ad/adc647981d1247b6a2dad1e35ab7a742.gif) je casti kazdeho z intervalu
je casti kazdeho z intervalu 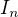 ,
, 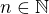 .
.
sneakfastem uvedena veta se velice dobre hodi k nadhernemu dukazu o nespocetnosti mnoziny vsech realnych cisel pomoci trisekce jednotkoveho intervalu.
Offline