Matematické Fórum

marram · 22. 01. 2012 16:37

Ahoj, obracím se na Vás a prosím o radu,
mám zadání příkladu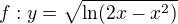
$f:y=\sqrt{\ln (2x-x^{2})}$
Potřebuji určit definiční obor, tak jsem začala s podmínkama:
$2x-x^{2} > 0$ , to mi vyšel interval $(0;2)$ . (už ted si nejsem jistá :D )
A jako druhou podmínku 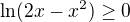$\ln (2x - x^{2}) \ge 0$ a tady už si nejsem jistá vůbec.
Výsledný definiční obor by měl vyjít 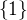$\{1\}$ . A ať to zkouším, jak to zkouším ne a ne se k té 1 dokopat :(
Poradíte mi, prosím někdo?

Aquabellla · 22. 01. 2012 17:44

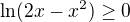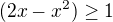$\ln (2x - x^{2}) \ge 0$ => $(2x - x^{2}) \ge 1$ - když si načrtneš graf logaritmu, tak to z toho uvidíš.

Matematické Fórum

#1 22. 01. 2012 16:37

Definiční obor přirozeného logaritmu pod odmocninou

#2 22. 01. 2012 17:44

Re: Definiční obor přirozeného logaritmu pod odmocninou

Zápatí