Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » pravdepodobnost: priklady (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 09. 2008 14:25
pravdepodobnost: priklady
ahoj lidicky, potreboval bych pomoc s dalsimi priklady:
1. Velitel má vyslat 5 lidí na stráž. O tom, kdo půjde se rozhodne losem. Pravděpodobnost, že na stráž půjdou určití 2 vojáci se rovná 2 / 87. Kolik můžů má četa?
2. Obdélník, s rozměry 14 m a 8 m, je namátkové pro?at přímkou m kolmou k úhlopříčce AC. Určete pravděpodobnost, že z obdélníku vzniknou dva lichoběžníky! Řešte tuto úlohu pro případ, že přímka m protíná úhlopříčku AC pod úhlem 60°!
3. Tři střelci vystřelili na cíl. Pravděpodobnost zásahu jednotlivých střelců je P1 = 0,8; P2 = 0,7; P3 = 0,4. Cíl byl zasažen jedním střelcem. Určete pravděpodobnost, že byl cíl zasažen:
a) prvním střelcem
b) druhým střelcem
c) třetím střelcem
Řešte tuto úloho také za předpokladu, že třetí střelec střílel dvakrát!
diky moc.
Offline
#2 25. 09. 2008 14:53
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: pravdepodobnost: priklady
1)Počet lidí označme n. Případů, kdy jsou dva vojáci ve stráži je (n-2 nad 3), protože k nim vybírám zbylé 3 z n-2 lidí. Celkem možných stráží je (n nad 5). To vede na rovnici
(n-2 nad 3):(n nad 5)=20/(n(n-1))=2/87
870=n(n-1)
n=30
2)Sestrojíme ten obdélník. Množinu všech možných průsečíků náhodné přímky s AC je celá úhlopříčka AC. Množinou průsečíků, které vyhoví je úsečka XY, kde X,Y jsou paty kolmic z B,D na AC. Spočteme délku XY a délku AC, naše pravděpodobnost je |XY|/|AC|. Pro 60˚ je akorát potřeba změnit konstrukci bodů XY.
3)Tady moc nevím, co počítat. Může být cíl zasažen dvěma střelci najednou? Pokud ano, pak jsou pravděpodobnosti stále 0,8, 0,7 0,4.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 25. 09. 2008 15:07 — Editoval ttopi (25. 09. 2008 15:15)
Re: pravdepodobnost: priklady
Ta 3 se řeší pomocí Bayesova vzorce.
Šance, že náhodně vybraný střelec trefí terč je 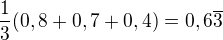 .
.
Pravděpodobnost, že zasáhl terč určitý střelec se pak vypočte jako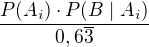
čili:
a)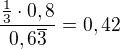
b)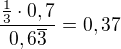
c)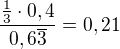
Pokud si to mohu dovolit, tak ten přídavek u 3 převedu na případ, že střílejí 4 střelci, přičemž 3. a 4. mají oba 0,4 pravděpodobnost, že trefí (jinak si neumím představit, že někdo vystřeli 2x, protože zatímco vystřelí poprvé, ostatní to taky zkusí a pak už třeba nebude muset střílet).
Takže ve jmenovateli bude místo 0,6 nově 0,575.
Potom:
a)P=0,348
b)P=0,304
c)P=0,174 - Tady je potřeba říct, že nevím, jaká je výsledná P, jestli je to 2*0,174=0,348, zřejmě jo.
oo^0 = 1
Offline
#4 25. 09. 2008 15:24
Re: pravdepodobnost: priklady
1. Mějme kouli o poloměru r a dále mějme pravidelný čtyřstěn, který je do této koule vepsán. Jaká je pravděpodobnost, že když náhodně umístíme dovnitř koule dva body, že budou tyto body ležet uvnitř čtyřstěnu.
2. Koule označená pravděpodobnostmi p a 1-p se nachází v první nebo v druhé urně. Pravděpodobnost toho, že se koule vytáhne z urny, ve které je uložena, je P(P≠1). Jaké je potřeba zvolit pravidlo pro n-násobný výběr z libovolné urny, aby byla pravděpodobnost maximální, že bude vytažena označená koule, vrací-li se zpět do urny.
3. Telegrafické znaky se skládají ze signálů „tečka“ a „čárka“. Je statisticky zjištěno, že se zkomolí 2/5 sdělení „tečka“ a 1/3 sdělení „čárka“. Dále je známo, že signály se používají v poměru 5:3. Určete pravděpodobnost, že byl přijat správně signál, jestliže:
a) byl přijat signál „tečka“
b) byl přijat signál „čárka“
Offline
#5 25. 09. 2008 15:28 — Editoval BrozekP (25. 09. 2008 15:47)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: pravdepodobnost: priklady
↑ ttopi:
Seš si jistý, že jsi ten vzorec použil správně? Mě vychází něco jiného ( a) , b)
, b) , c)
, c) ), za chvíli napíšu postup.
), za chvíli napíšu postup.
Použiju vzorec pro podmíněnou pravděpodobnost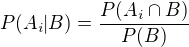
Hledáme pravděpodobnost toho, že se trefil i-tý střelec (to je jev 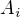 ) za předpokladu, že se trefil právě jeden střelec (jev B).
) za předpokladu, že se trefil právě jeden střelec (jev B).
Jev 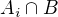 znamená, že se trefil i-tý střelec a ostatní se netrefili, jeho pravděpodobnost je tedy
znamená, že se trefil i-tý střelec a ostatní se netrefili, jeho pravděpodobnost je tedy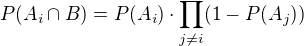
Pravděpodobnost toho, že se trefil právě jeden je zřejmě součtem pravděpodobností, že se trefil pouze první, pouze druhý...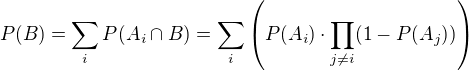
Pravděpodobnost, že zasáhl i-tý střelec, pokud víme, že zasáhl právě jeden, je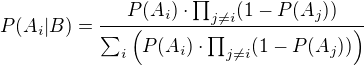
V případě tří střelců tak máme (pokud označíme 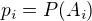 )
)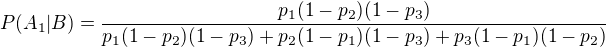
a podobně pro další dva. Vychází mi pak pravděpodobnosti
Stejný vzorec mi vychází, pokud to udělám Bayesovým vzorcem.
Offline
#6 25. 09. 2008 15:34
Re: pravdepodobnost: priklady
Kondr: Můžeš mi prosímtě vysvětlit znovu tu 2?
Podle mě je to tak, že šance, že budou nějací 2 vojaci vybráni je 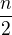 , tedy kombinace, protože je jedno, kterýho z nich vyberu dřív, nezáleži na pořadí.
, tedy kombinace, protože je jedno, kterýho z nich vyberu dřív, nezáleži na pořadí.
K nim přijdou ještě 3 vojáci ze zbytku. Opět nezáleží na pořadí, takže 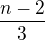 .
.
Tyto výrazy se mezi sebou násobí.
Mě tedy vychází 
Když dosadím za n=30, vyjde mi nesmysl.
oo^0 = 1
Offline
#7 25. 09. 2008 16:07 — Editoval ttopi (25. 09. 2008 16:11)
Re: pravdepodobnost: priklady
Musím s odstupem času uznat, že tam asi musí hrát roli ta podmíněná pravděpodobnost, protože to, že byl terč trefen 1x se v mém výpočtu nevyskytuje, přitom je to podstatné.
Moje řešení by platilo, pokud bychom se ptali na to, jaká je P, že šíp vyndaný z terče (BEZ OHLEDU NA TO, KOLIK JICH V NĚM JE) patří střelci 1,2 nebo 3.
Už je mi to tedy jasné a omlouvám se.
oo^0 = 1
Offline
#8 25. 09. 2008 16:41 — Editoval BrozekP (25. 09. 2008 16:42)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: pravdepodobnost: priklady
↑ ttopi:
Myslím, že tvoje řešení by neplatilo ani v tomto případě. Pravděpodobnost, že šíp vytažený z terče je prvního střelce je rovna součtu následujících pravděpodobností:
- jako jediný se trefil, pak je jistě vytažen jeho šíp. To má pravděpodobnost 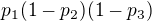 .
.
- trefil se on a ještě druhý střelec. Je poloviční pravděpodobnost, že vytáhneme šíp prvního střelce. Tomu odpovídá pravděpodobnost 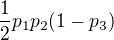 .
.
- trefil se on a ještě třetí střelec. Je poloviční pravděpodobnost, že vytáhneme šíp prvního střelce. Tomu odpovídá pravděpodobnost  .
.
- trefili se všichni. Je třetinová pravděpodobnost, že vytáhneme šíp prvního střelce. Tomu odpovídá pravděpodobnost 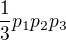 .
.
Pravděpodobnost, že vytáhneme šíp prvího střelce je tedy 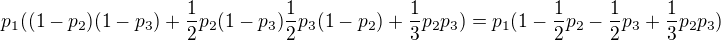
Pro tři střelce vychází pravděpodobnosti 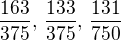 . Do jedné zbývá pravděpodobnost
. Do jedné zbývá pravděpodobnost 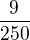 , což odpovídá pravděpodobnosti toho, že se nikdo netrefí.
, což odpovídá pravděpodobnosti toho, že se nikdo netrefí.
Offline
#9 25. 09. 2008 16:48
Re: pravdepodobnost: priklady
Tak to už se mi přestává zdát. My jsme Bayesův vzorec používali i bez podmíněné pravděpodobnosti a příklady nám vycházely. Jako vzorový jsme měli příklad se semínkama, který je principielně stejný jako tento.
oo^0 = 1
Offline
#10 25. 09. 2008 17:01 — Editoval BrozekP (25. 09. 2008 17:44)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: pravdepodobnost: priklady
↑ ttopi:
Napiš ten se semínkama a můžeme ho rozebrat, proč se to liší.
↑ theodore:
K příkladu 3 z druhé série. Zavedu si nějaké značení - jev  znamená odeslaná tečka,
znamená odeslaná tečka,  odeslaná čárka,
odeslaná čárka, 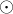 přijatá tečka a
přijatá tečka a  přijatá čárka. Pak ze zadání víme:
přijatá čárka. Pak ze zadání víme:
V případě a) se nás ptají na 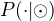 , v případě b) nás zajímá
, v případě b) nás zajímá 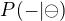
Teď stačí použít Bayesův vzorec a máš to. Když se to takhle rozepíše, tak myslím ani není moc nad čím přemýšlet. Mě vyšlo a) 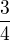 a b)
a b)  .
.
Príklad 1 z druhé série:
Zřejmě je těžiště čtyřstěnu ve středu koule. Z trojúhelníku tvořeného dvěma vrcholy čtyřstěnu a středu hrany spojující zbylé dva vrcholy zjistíme, že pro výšku v čtyřstěnu platí 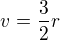 . Není těžké odvodit, že mezi výškou pravidelného čtyřstěnu a jeho hranou
. Není těžké odvodit, že mezi výškou pravidelného čtyřstěnu a jeho hranou  platí vztah
platí vztah  . Pro objem pravidelného čtyřstěnu máme vzorec
. Pro objem pravidelného čtyřstěnu máme vzorec 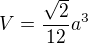 (není těžké jej odvodit). Po dosazení
(není těžké jej odvodit). Po dosazení 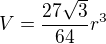 . Objem koule je
. Objem koule je 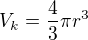 . Pravděpodobnost, že jeden bod bude v čtyřstěnu je tedy
. Pravděpodobnost, že jeden bod bude v čtyřstěnu je tedy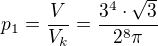
Dva body umis?ujeme nezávisle na sobě, pravděpodobnost toho, že budou oba v čtyřstěnu je tedy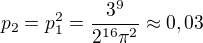
Offline
#11 25. 09. 2008 19:05 — Editoval BrozekP (25. 09. 2008 19:05)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: pravdepodobnost: priklady
↑ theodore:
Příklad 2 z druhé série:
Zadání je trochu divně formulované, doufám, že to má být to samé jako:
Označená koule se s pravděpodobnostmi p a 1-p nachází v první nebo v druhé urně. Pravděpodobnost toho, že se koule vytáhne z urny, ve které je uložena, je P(P≠1). Jaké je potřeba zvolit pravidlo pro n-násobný výběr z libovolné urny, aby byla pravděpodobnost maximální, že bude vytažena označená koule, vrací-li se zpět do urny.
Zajímá nás pravděpodobnost toho, že se koule po a tazích z první urny a b tazích z druhé urny nachází v první urně, za předpokladu, že ještě nebyla vytažena. Pokud pravděpodobnost bude větší než polovina, náš další tah bude z první urny, pokud bude menší než polovina, náš další tah bude z druhé urny (pokud bude jedna polovina, pak je jedno, kterou urnu vybereme).
Symbolem 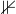 budu značit jev, že koule je v první urně a symbolem
budu značit jev, že koule je v první urně a symbolem 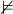 , že je v druhé urně. Je tedy
, že je v druhé urně. Je tedy 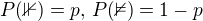 . Symbolem
. Symbolem 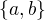 budu značit jev, že označená koule nebyla vytažena po a tazích z první a b tazích z druhé urny. Podle Bayesova vzorce je
budu značit jev, že označená koule nebyla vytažena po a tazích z první a b tazích z druhé urny. Podle Bayesova vzorce je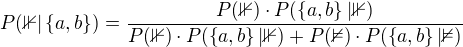
Zbývá tedy určit 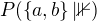 a
a  . Pravděpodobnost, že označená koule nebyla vytažena po a tazích z první a b tazích z druhé urny za předpokladu, že je v první urně je zřejmě
. Pravděpodobnost, že označená koule nebyla vytažena po a tazích z první a b tazích z druhé urny za předpokladu, že je v první urně je zřejmě 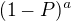 , za předpokladu, že je v druhé urně je to
, za předpokladu, že je v druhé urně je to  . Je tedy
. Je tedy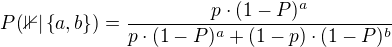
Na začátku je  . V každém kroku vyčíslíme uvedený výraz a zjistíme zda je větší než polovina a podle toho se rozdhodneme, z které urny tahat.
. V každém kroku vyčíslíme uvedený výraz a zjistíme zda je větší než polovina a podle toho se rozdhodneme, z které urny tahat.
Offline
#12 25. 09. 2008 23:31
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: pravdepodobnost: priklady
↑ ttopi:
Pár drobností k tvému řešení:
- kombinační čísla piš pomocí \choose, s tím \frac to působí jako zlomek.
- nejde nám o to spočítat počet možností, jak stráž vybrat, ale o spočítání pravděpodobnosti, kombinační čísla se musí něčím dělit.
- dvojici, pro kterou chceme pravděpodobnost počítat máme pevně danou, žádné (n nad 2) tam proto nebude.
Řekněme, že máme 30 vojáků. Nejprve spočítejme takové pětice, že první dva jsou v pětici. Těch je (28 nad 3)=(28*27*26)/6.
Celkem je pětic (30 nad 5)=(30*29*28*27*26)/(120). Když tato dvě čísla podělím, dostanu
20/(30*29)=2/87.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#13 26. 09. 2008 07:04
Re: pravdepodobnost: priklady
↑ Kondr:
Zdravím.
Za ty zlomky se samozřejmě omlouvám, vůbec mě to netrklo, ale samozřejmě je to moje chyba.
Dal jsem n nad 2, protože jsem myslel, že ta dvojice není pevně daná, že je to prostě náhodné. Respektive že někdo to ví, ale já, který to počítám nevím.
Díky za osvětu :-)
oo^0 = 1
Offline
#14 22. 10. 2018 15:54
Re: pravdepodobnost: priklady
↑ Pavel Brožek:
Dobrý den, prosím, nevíte, jak tuto úlohu řešit s tím dodatkem, že ji máme řešit i za předpokladu, že 3. střelec vystřelil dvakrát?
Děkuji!
Offline
#15 22. 10. 2018 16:38
Re: pravdepodobnost: priklady
↑ Johana16:
Zdravím.
Řekl bych, spočítat pravděpodobnost zásahu třetím střelcem při dvou výstřelech a tu použít při přepočítání úlohy podle původního postupu.
Pokud se tedy nemýlím.
Offline
#16 22. 10. 2018 17:37
Re: pravdepodobnost: priklady
↑ Jj:
Takže
P(B1) = 0,8*0,3*0,6*0,6 (pst,že se trefil první střelec)
P (B2) = 0,2*0,7*0,6*0,6 (pst, že se trefil druhý střelec)
P (B3) = 0,2*0,7*0,6*0,4 (pst, že se třetí střelec při jedné ze svých 2 střel)
Jak ale určím
P(A/B1) = (pst, že je v terči jeden zásah za podmínky, že se trefil 1. střel)
a obdobně pro P(A/B2) a P(A/B3)? Děkuji
Offline
#17 22. 10. 2018 20:21 — Editoval Jj (22. 10. 2018 20:26)
Re: pravdepodobnost: priklady
↑ Johana16:
Pravděpodobnost počtu zásahů (X) třetího střelce bych viděl takto:
P(X = 0) = 0.6*0.6 = 0.36
P(X = 1) = 0.4*0.6 + 0.6*0.4 = 0.48
P(X = 2) = 0.4*0.4 = 0.16
(součet = 1.00)
Asi uvažujete že třetí střelec se také může trefit max. jednou. Nezdá se mi to nutné, ale budiž. Pak
P(B1) = 0,8*0,3*0.36 (pst, že se trefí jen první střelec)
P (B2) = 0,2*0,7*0.36 (pst, že se trefí jen druhý střelec)
P (B3) = 0,2*0,7*0.48 (pst, že se trefí jen třetí střelec při jedné ze svých 2 střel)
Pravděpodobnost, že cíl bude zasažen (jednou střelou) P(B) = P(B1)+P(B2)+P(B3),
pak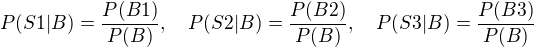
Pokud se tedy nemýlím.
Offline
#18 23. 10. 2018 16:47
Re: pravdepodobnost: priklady
↑ Jj:
A ty jednotlivé pravděpodobnosti se už nebudou ničím přenásobovat?
Dle Bays. vzorce by se měly, ale moc nerozumím čím.
https://wikimedia.org/api/rest_v1/media … 371fe85a28
Offline
#19 23. 10. 2018 18:28 — Editoval Jj (23. 10. 2018 18:29)
Re: pravdepodobnost: priklady
↑ Johana16:
Ne, už žádné násobení, platí:  , v čitatelích máme průnik jevů (trefí konkrétní střelec, ostatní nic).
, v čitatelích máme průnik jevů (trefí konkrétní střelec, ostatní nic).
V podstatě totéž, jako tady ↑ Pavel Brožek:, jen třetí střelec má jinou pravděpodobnost.
Pokud se tedy nemýlím.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » pravdepodobnost: priklady (TOTO TÉMA JE VYŘEŠENÉ)