Matematické Fórum

Ryco · 26. 01. 2012 19:53 — Editoval Ryco (26. 01. 2012 20:15)

Na sociální síti fixlbook se platí vstupní poplatek jehož velikost má 2 čáasti. Fixní část je 7dolaru a pohyblivá část je 1dolaru za každého dříve přihlášeného člena. První člen tak zaplatí 7dolaru, druhý 8dolaru, třetí 9dolaru atd. Mat. indukcí dokažte, že za n členů vybere pokladník n(n+13)/2dolaru.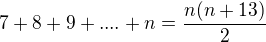

$7+8+9+ .... +n=\frac{n(n+13)}{2}$

indukční základ pro n=1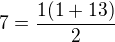
$7=\frac{1(1+13)}{2}$
$7=7$

indukční krok 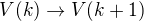$V(k) \rightarrow V(k+1)$
$7+8+9+ .... +k=\frac{k(k+13)}{2}$

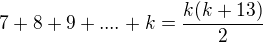
indukční předpoklad
$7+8+9+ .... +k+k+1=\frac{(k+1)(k+14)}{2}$
$\frac{k(k+13)}{2}+k+1=\frac{(k+1)(k+14)}{2}$
$k(k+13)+2k+2=(k+1)(k+14)$
$k^{2}+13k+2k+2=k^{2}+14+k+14$
$k^{2}+15k+2=k^{2}+15k+14$

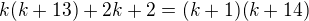
Indukční předpoklad neplatí

Může mi to někdo pls zkontrolovat? myslím si že sem někde udělal chybu ale nemůžu ji najít

no jak se tak na to ted divam tak divam tak uz indukcni zaklad mam spatne. Navic napada me jestli neni v zadani preklep jestli nemela byt prava strana pouze $\frac{n(n+1)}{2}$ potom by to nejspis vychazelo.

jarrro · 26. 01. 2012 20:49 — Editoval jarrro (27. 01. 2012 17:59)

↑ Ryco:problém je asi v tom,že ak má byť posledný člen n tak to neplatí
platí,že súčet prvých n členov tej postupnosti je taký ako si uviedol teda
$\sum\limits_{i=0}^{n-1}{\left(7+i\right)}=\frac{n\left(n+13\right)}{2}\nl 7=\frac{1\left(1+13\right)}{2}\nl \sum\limits_{i=0}^{n}{\left(7+i\right)}\stackrel{IP}{=}\frac{n\left(n+13\right)}{2}+7+n=\frac{n\left(n+13\right)+2n+14}{2}\nl=\frac{\left(n+1\right)\left(n+14\right)}{2}$

Rumburak

Ahoj, mně to vycházi
$7+8+9+ .... +k= (1+2+ ...+k) - (1+2+...+6) = \\= \frac{k(k+1)}{2} - \frac{6\cdot 7}{2} = \frac{k^2 + k - 6\cdot 7}{2} =\frac{(k + 7)(k - 6)}{2}$ ,

což je, jak teď vidím, ve shodě s výsledkem, ke kterému došel ↑ jarrro: pro $n = k-7$ .

Matematické Fórum

#1 26. 01. 2012 19:53 — Editoval Ryco (26. 01. 2012 20:15)

Důkaz matematickou indukcí

#2 26. 01. 2012 20:49 — Editoval jarrro (27. 01. 2012 17:59)

Re: Důkaz matematickou indukcí

#3 27. 01. 2012 15:31 — Editoval Rumburak (27. 01. 2012 15:43)

Re: Důkaz matematickou indukcí

Zápatí