Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 01. 2012 20:05
Příklad ze státní maturity

Dobrý den,
dodělávám řešení příkladů ze státní maturity vyšší verze.
http://www.nabla.cz/obsah/matematika/statni-maturita/
S tímto příkladem si však moc nevím rady. Přesněji řečeno, nechce se mi to dostudovávat.
Mohl by mi ho, prosím, někdo vypočítat. Byl bych Vám moc vděčný. Ušetří mi to spoustu času.
P. S.: Použití obrázků mám od Cermatu písemně povoleno.
Fyzika a matematika konečně srozumitelně - www.nabla.cz
Fyzikální bludy
Řešení státní maturity z matematiky
Kdy psát mě a mně
Offline
#3 27. 01. 2012 21:43
Re: Příklad ze státní maturity
Offline
#4 27. 01. 2012 21:46
Re: Příklad ze státní maturity
Zdravím,
tímhle příkladem jsem se před časem zabýval. A za sebe říkám, že tenhle příklad CERMAT trošku přestřelil.
část 1.) Postupně počítáme následující člen dosazením předchozí do rekurentního zadání. Celé to děláme obecně.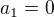




....
část 2.) Tady jsem nepřišel na řešení, dle výsledků cermatu musí být |q| < 1, jako pro normální geometrickou posloupnost. Ale netuším, jak na to přijít. Moje úvaha vypadala asi nějak takto: Aby byla posloupnost konvergentní, musí existovat součet členů posloupnosti. Při drobné úvaze lze napsat začátek součtu nějak takto:  Kde si ty závorky můžeme představit jako nějaké úplně jiná
Kde si ty závorky můžeme představit jako nějaké úplně jiná  , pro které musí platit:
, pro které musí platit:  .
.
U tohoto fakt nevím, pokud někdo ví, budu rád, když napoví.
část 3) Pokud si napíšeme členy tímto způsobem, lze uhodnout vzorce pro n-tý člen (zkoušel jsem vzorec pro n-tý člen vypočítat, ale to se mi nepodařilo).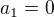




...
A máme vypočítat limitu pro q = -0,5:
Kde v závorce je vlastně součet nekonečné geometrické řady, jejíž součet je:
Tedy: 
Zajímalo by mě vzorové řešení té druhé části.
Offline
#5 27. 01. 2012 21:51
Re: Příklad ze státní maturity
↑ Annnnnd:
Koukám na tvé řešení k druhé části úlohy: rovnou tam píšeš, že aby byla konvergentní, musí platit  . Toto ale platí u geometrické posloupnosti a toto GP není. Můžeme si to dovolit tvrditi u této posloupnosti? Také jsem o tom uvažoval a díky tomu mě ten příklad docela otrávil :-)
. Toto ale platí u geometrické posloupnosti a toto GP není. Můžeme si to dovolit tvrditi u této posloupnosti? Také jsem o tom uvažoval a díky tomu mě ten příklad docela otrávil :-)
Offline
#6 27. 01. 2012 22:11
Re: Příklad ze státní maturity
↑ smatel:jestli oni tim nemysli obecnou posloupnost. a clovek si musi uvedomit ze konvergence plati u GP. cili |q|<1 . a urcim interval. Protoze pro zadanou posloupnost rekurentnim vztahem kde a1=0 neni mozne aby a2 byla nejaka hodnota ruzna od 0 v GP.
Offline
#7 27. 01. 2012 22:39
Re: Příklad ze státní maturity
↑ Annnnnd:
Zdravím. No v zadání mají jasně dáno, kdy je poslounpst  konvergentní a tuto posloupnost mají v zadání přesně zadanou rekurentě. Takže GP obecně asi spíše nemyslí - a pokud jo, tak by mě pěkně namíchli, protože jsem nad tím nějakou tu hodinu strávil :-).
konvergentní a tuto posloupnost mají v zadání přesně zadanou rekurentě. Takže GP obecně asi spíše nemyslí - a pokud jo, tak by mě pěkně namíchli, protože jsem nad tím nějakou tu hodinu strávil :-).
Kdy je posloupnost konvergentní = tehdy, kdy má limitu (vlastní). U GP je požadavek na q. Ale to neznamená, že neexistují jiné posloupnosti, které se v nekonečnu k něčemu blíží. A tato GP není.
Díky za konzultaci :-)
Offline
#8 27. 01. 2012 23:03
Re: Příklad ze státní maturity
no to mas pravdu. oni zde se nebavi o zadne GP. resp. jde o to aby posloupnost mela limitu. cili ja bych to bral jako an = 4 + 4q + 4q^2 + 4q^3 + 4q^4 +..... 4q^n-2 .... a aby toto melo vlastni hodnotu, kdyz se n bude blizit k nekonecnu a existoval ten soucet tak q musi byt elementem (-1;1). resp |4q / 4| < 1 . ono to je takovy na hlavu a clovek se do toho snadno zamota.
Offline
