Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » slovné úlohy na derivácie: určovanie lokálneho maxima alebo minima (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 01. 2012 21:27
slovné úlohy na derivácie: určovanie lokálneho maxima alebo minima
Opäť sa jedná o úlohy na derivácie zo zbierky úloh.
v úlohách sa pri výpočte overuje, či ide o lokálne maximum alebo minimum:
napr. strana 64
Jelikož na intervalu  je funkce S´(x) rostoucí a na intervalu
je funkce S´(x) rostoucí a na intervalu  je S´(x) klesající, má funkce S(x) v hodnotě 400/(pi+4) své maximum.
je S´(x) klesající, má funkce S(x) v hodnotě 400/(pi+4) své maximum.
derivácia je  a z nej viem vyčísliť druhú deriváciu.
a z nej viem vyčísliť druhú deriváciu.
V prípadoch, kde je výsledkom úlohy konkrétne číslo, sa mi zdá lepšie urobiť teda ešte druhú deriváciu a na jej základe určiť, či ide o minimum alebo maximum. Môžem to teda overovať takto t.j. druhou deriváciou ?
Ak výsledkom úlohy nie je číslo, ale nejaký nevyčíslený výraz, tak tu si už nie som taký istý
napr. strana 66
Jelikož na intervalu ![kopírovat do textarea $(-\infty, \sqrt[3]{a^2b})$](/mathtex/14/14907b77078e7a67ee064edf188c1755.gif) je funkce l´(x) klesající a na intervalu
je funkce l´(x) klesající a na intervalu ![kopírovat do textarea $(\sqrt[3]{a^2b},+\infty)$](/mathtex/09/094a049daf866e05c1f6a5939b9a8883.gif) je l´(x) rostoucí, má funkce l(x) v hodnotě
je l´(x) rostoucí, má funkce l(x) v hodnotě ![kopírovat do textarea $\sqrt[3]{a^2b}$](/mathtex/de/debc5c1d9112df0753a17b02d0d11605.gif) své minimum.
své minimum.
derivácia z tohto príkladu je 
Druhá derivácia mi však už nič nepovie, lebo výsledkom nie je číslo (aspoň sa mi vidí, že nie je).
Akým spôsobom potom zistím, že funkcia je naozaj v jednej celej polovici intervalu klesajúca a v druhej zas rastúca ?
Definícia rastúcej a klesajúcej funkcie, kde pre každé  resp.
resp.  mi tu nejako nepomáha. Ako to mám overiť pre celý nekonečný interval ?
mi tu nejako nepomáha. Ako to mám overiť pre celý nekonečný interval ?
ďakujem za rady
Offline
- (téma jako vyřešené označil(a) etchie)
#2 27. 01. 2012 10:34 — Editoval jardofpr (27. 01. 2012 16:07)
Re: slovné úlohy na derivácie: určovanie lokálneho maxima alebo minima
↑ etchie:
môžeš to zisťovať aj druhou deriváciou, ale nemusíš vždy dostať odpoveď,
môže sa stať že vyjde aj druhá derivácia rovná 0, a potom to budeš musieť buď derivovať znova,
kým nenatrafíš na nejakú nenulovú deriváciu, čo môźe trvať dlho, alebo aj tak použiť tú metódu, ktorú používajú v tvojej zbierke..
užitočnejšie sa mi zdá určovať to teda pomocou znamienok (vo všeobecnosti)
to sa týka aj úlohy zo strany 66
okrem toho zrovna tento príklad tam riešia s chybami
po nájdení derivácie a nulového bodu píšu
veta v červenom rámčeku (aj ten obrázok nad ňou) je blbosť
definičný obor derivácie funkcie (ako funkcie l'(x)) je podmnožinou definičného oboru pôvodnej funkcie
funkcia  nie je definovaná v bode
nie je definovaná v bode  a preto tam
a preto tam
nemôže byť definovaná ani jej derivácia (to je vidno aj z menovateľa derivácie ako je tam opísaná)
a tieto fakty treba by vyšetrovaní priebehu funkcie (kam zisťovanie extrémov rozhodne patrí) vždy brať do úvahy
okrem toho, z prvej derivácie zistíme či je klesajúca alebo rastúca funkcia  , nie funkcia
, nie funkcia  ,
,
funkcia môže byť záporná a pritom kľudne rastúca, a podobne ..
toľko k tomu červenému rámčeku
okrem toho je funkcia l(x) do svojej podoby zostavená len pre  a v ďalšom riešení by sa k nej malo tak aj pristupovať
a v ďalšom riešení by sa k nej malo tak aj pristupovať
ďalším faktom je že sa by sa táto úloha ako aplikácia derivácie na tento problém mala riešiť pre  čo tam tiež nikde nie je spomenuté
čo tam tiež nikde nie je spomenuté
(nebudeme predsa brať do úvahy kanály s nulovou alebo zápornou šírkou)
začínať by sa malo teda s hľadaním extrému funkcie 
prvá derivácia a jej nulový bod budú potom ![kopírovat do textarea $l'(x)=\frac{x^3-a^2b}{x^2\sqrt{x^2 + a^2}} \,,\, x_{0}=\sqrt[3]{a^2b}$](/mathtex/09/09e1086b8109009c3a596222cff82435.gif)
ak by si chcel druh extrému zisťovať z druhej derivácie
keďže  , na intervale
, na intervale 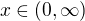 platí
platí 
a keďže ![kopírovat do textarea $\sqrt[3]{a^2b} \in (0,\infty)$](/mathtex/c1/c18e68b0ba34f37f80d67b910dca4cad.gif) je aj
je aj 
a funkcia  má v bode
má v bode ![kopírovat do textarea $x_{0} = \sqrt[3]{a^2b}$](/mathtex/68/68909d3c171be61b005125a602e60e54.gif) lokálne minimum
lokálne minimum
Offline
#3 29. 01. 2012 11:44
Re: slovné úlohy na derivácie: určovanie lokálneho maxima alebo minima
↑ jardofpr:
mohol by si mi ukázať ako na to pomocou "užitočnejšie sa mi zdá určovať to teda pomocou znamienok (vo všeobecnosti)" ? podmienka mi dosť pomohla v uvažovaní pre tento konkrétny prípad. Neviem sa však prehrýzť cez situáciu kedy by v druhej derivácii neboli samé kládné znamienka, ale by sa to miešalo kladné a záporné. Vtedy zrejme neviem rozhodnúť, či výsledok je kladný, nulový alebo záporný. Lebo neviem vyčísliť hodnoty a, b. Je to tak ?
podmienka mi dosť pomohla v uvažovaní pre tento konkrétny prípad. Neviem sa však prehrýzť cez situáciu kedy by v druhej derivácii neboli samé kládné znamienka, ale by sa to miešalo kladné a záporné. Vtedy zrejme neviem rozhodnúť, či výsledok je kladný, nulový alebo záporný. Lebo neviem vyčísliť hodnoty a, b. Je to tak ?
ďakujem
Offline
#4 29. 01. 2012 13:37 — Editoval jardofpr (29. 01. 2012 13:46)
Re: slovné úlohy na derivácie: určovanie lokálneho maxima alebo minima
↑ etchie:
keď sa to nedá určiť jednoznačne, malo by to ísť aspoň určiť v závislosti na parametroch a,b
ale to by sa zrejme nemalo stávať pri týchto slovných úlohách
čo sa týka toho určovania extrému pomocou prvej derivácie,
zisťuje sa, aké má znamienko derivácia naľavo od nulového bodu a napravo od nulového bodu,
ozn  nulový bod derivácie, teda
nulový bod derivácie, teda 
1.)ak je  pre
pre  a
a  pre
pre  funkcia f(x) má v bode
funkcia f(x) má v bode  ostré lokálne minimum
ostré lokálne minimum
2.)ak je  pre
pre  a
a  pre
pre  funkcia f(x) má v bode
funkcia f(x) má v bode  ostré lokálne minimum
ostré lokálne minimum
3.)ak je znamienko derivácie na oboch stranách bodu  rovnaké, funkcia v tom bode nemá extrém
rovnaké, funkcia v tom bode nemá extrém
Pozn.
(existencia (obojstrannej) derivácie funkcie f v bode  zaručuje, že
zaručuje, že  okrem toho že patrí do def.oboru f je aj hromadným bodom definičného oboru funkcie f, a teda exisuje nejaký otvorený interval
okrem toho že patrí do def.oboru f je aj hromadným bodom definičného oboru funkcie f, a teda exisuje nejaký otvorený interval  tak, že
tak, že  je jeho vnútorným bodom
je jeho vnútorným bodom
uvedené 1)2)3) platí pre  )
)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » slovné úlohy na derivácie: určovanie lokálneho maxima alebo minima (TOTO TÉMA JE VYŘEŠENÉ)
