Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita rekurentne zadane posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)
#1 27. 09. 2008 14:41
Limita rekurentne zadane posloupnosti
Ahoj vsichni, abych si dal taky na chvilku pokoj od neustaleho napominani zdejsich uzivatelu, tak se take na neco zeptam. Nedavno jsme tady s Pavlem hovorili o retezovem zlomku pro zlaty rez: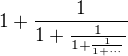
Ja jsem hodnotu zlomku nasel hledanim korenu rovnice 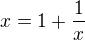
Coz je po uprave znama kvadraticka rovnice, jejiz kladny koren je prave zlaty rez. Tato rovnice ma ale jeste zaporny koren. Na zaklade jake uvahy jsme tento zaporny koren vyloucili jako hodnotu toho retezoveho zlomku? Nebo chcete-li jako limitu posloupnosti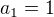

?
Zjistil jsem, ze mam znacne mezery prave v pocitani limit rekuretne zadanych posloupnosti, cili kdyby byl nekdo ochoten to osvetlit...
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#2 27. 09. 2008 15:11 — Editoval BrozekP (27. 09. 2008 15:17)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limita rekurentne zadane posloupnosti
↑ Lishaak:
Pokud limita této posloupnosti existuje (označíme ji A), pak podle aritmetiky limit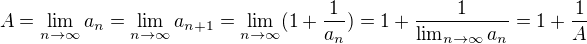
Limita tedy splňuje uvedenou rovnici. Řešením kvadratické rovnice získáme dva kořeny, jeden je ale záporný, ten můžeme tedy vyloučit (zřejmě totiž platí  a tedy všechny členy jsou podle matematické indukce kladné).
a tedy všechny členy jsou podle matematické indukce kladné).
Jestliže limita existuje, pak je nutně rovna 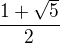 .
.
Zbývá ukázat, že posloupnost limitu má. Zkusím se na to ještě podívat, teď mě nic jednoduchého nenapadá.
Offline
#3 27. 09. 2008 16:06 — Editoval Marian (27. 09. 2008 16:10)
Re: Limita rekurentne zadane posloupnosti
↑ BrozekP:
Existuje dokonce kriterium pro konvergenci nekonečných řetězových zlomků (věta 10, str. 10 v následující knize). Vynikající knihou k této tematice je pak dílo Chinčina "Řetězové zlomky". Dá se stáhnout třeba zde (djvu).
Offline
#4 27. 09. 2008 16:11
Re: Limita rekurentne zadane posloupnosti
Ok, prokazali jsme, ze vsechny cleny jsou kladne, tedy limita bude nezaporna (pokud existuje). Ale co treba takovyto priklad.
Uvazujme posloupnost zadanou rekuretne:
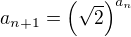
Budeme-li resit rovnici 
Obdrzime dva koreny, x = 2 a x = 4. Oba dva jsou kladne, vsechny cleny posloupnosti jsou taky klade, jak nyni rozhodneme, ktere z cisel je limitou?
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#5 27. 09. 2008 16:15 — Editoval Pavel (27. 09. 2008 16:16)
Re: Limita rekurentne zadane posloupnosti
↑ BrozekP:
Stačí ukázat, že vybraná posloupnost s lichými indexy je rostoucí a shora omezená a vybraná posloupnost se sudými indexy je klesající a zdola omezená. Obě vybrané posloupnosti mají limitu a tyto jsou si rovny.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 27. 09. 2008 16:20 — Editoval Marian (27. 09. 2008 16:26)
Re: Limita rekurentne zadane posloupnosti
↑ Lishaak:
Vzpomeneme si na Lambertovu W-funkci a najdeme hodnotu takové limity ve tvaru
Více třeba zde.
Offline
#7 27. 09. 2008 16:36
Re: Limita rekurentne zadane posloupnosti
Ano, to je urcite taky zpusob reseni, ale je to prilis ultimatni. Je bych spis potreboval osvetlit ten elementarnejsi postup, ktery jsem tady nastinil. Tu limitu (pokud prokazeme ze existuje) je prece mozne vypocitat jako reseni te mnou uvedene rovnice. Jeden koren je ale treba vynechat a ja nevim, podle jakeho kriteria se to rozhodne. Mozna se ptam nejasne, protoze mi nedochazi nejaky zasadni princip. Kdyby mel nekdo odkaz na material ohledne pocitani limit rekurentne zadanych posloupnosti, byl bych mu velmi vdecen za link.
Jinak dekuju Marianovi za odkaz na tu knizku o retezovych zlomcich. Skoda jen, ze posledni dobou mam uz tolik matematicke literatury, ze nevim co driv cist...
Nothing in the world that's worth having comes easy.
Always do what you are most afraid of.
Offline
#8 27. 09. 2008 17:15 — Editoval Pavel (27. 09. 2008 17:16)
Re: Limita rekurentne zadane posloupnosti
Stačí dokázat, že posloupnost je rostoucí, pokud je počáteční podmínka menší než 2. Pokud tato je větší než 2 a menší než 4, posloupnost je klesající. Limita v obou případech musí být rovna 2. Je-li počáteční podmínka větší než 4, má posloupnost limitu nekonečno. V obecném případě bude situace složitější.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#9 27. 09. 2008 17:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limita rekurentne zadane posloupnosti
↑ Pavel:
Ano, snažil jsem se o to, ale moc se mi to nedařilo. Teď už jsem na to ale přišel.
Očekávanou limitu značím 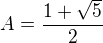 . Budu zkoumat funkci
. Budu zkoumat funkci  na intervalu
na intervalu ![kopírovat do textarea $[1,\,2]$](/mathtex/0f/0f46ae1341eed4387f605be9d89fbeff.gif) (je zajímavá, protože
(je zajímavá, protože 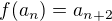 ). Tato funkce je zřejmě rostoucí. Dále platí
). Tato funkce je zřejmě rostoucí. Dále platí  a tedy
a tedy
Protože  a
a 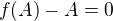 , platí
, platí
Z toho plyne ![kopírovat do textarea $f([1,\,2])\subset[1,\,2]$](/mathtex/87/87399c368bcede7bf50f1c99b9ac1a7b.gif) . Dále z
. Dále z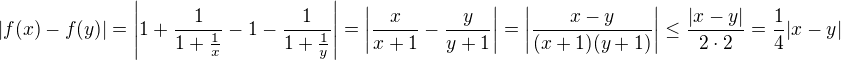
plyne, že f je kontrakce. Z důkazu Banachovy věty o pevném bodě plyne, že libovolná posloupnost definovaná prvním členem ![kopírovat do textarea $b_1\in[1,2]$](/mathtex/68/68928d12ed20b03c16bd29c7768a8cb3.gif) a
a 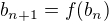 má limitu A.
má limitu A.
Protože 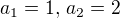 a
a 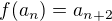 , pak podle předchozího je
, pak podle předchozího je
a tedy limita posloupnosti  existuje a je také rovna A.
existuje a je také rovna A.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita rekurentne zadane posloupnosti (TOTO TÉMA JE VYŘEŠENÉ)