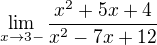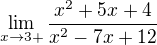Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 15. 11. 2007 23:57
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Limita funkce
Těmi nekonečny si jistý být můžeš. Čitatel jde v obou případech k 28, jmenovatel k 0. Výraz typu "nenula/nula" vyjde vždy plus nebo mínus nekonečno, záleží na znaménách čitatele a jmenovatele. Čitatel je v obou našich případech kladný.
Jmenovatel je kvadratická funkce, která protíná osu x v bodech 3 a 4 a je otevřená nahoru -
proto je na intervalu (3,4) záporná a na intervalech (-oo,3) a (4,oo) kladná. Proto je jmenovatel první limity kladný a druhé záporný.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#4 16. 11. 2007 10:18 — Editoval jelena (16. 11. 2007 10:19)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita funkce
Jeste doplneni a polopaticka rada (zdravim, Mariane, jsem si toho vedoma, ze polopaticka :-)
Kolega Kondr to vysvetlil cele, doplnim jen, ze pocitani limit zleva nebo zprava v bode nespojitosti (coz bod x = 3 skutecne je) je zpocatku trochu obtizne uchytitelne - delime prece nulou, tak proc ve stejnem bode + nekonecno, a hned na to - nekonecno.
Staci si predstavit, ze prichazime li k bodu nespojitoszi zleva, tj. z cisel o neco mensich nez 3, pak jsme na intervalu (-oo, 3), kde je jmenovatel kladny, pro presvedceni si dosadis do jmenovatele treba 2,9 a odhadnes pouze znamenko (polopaticky si rikam, ze delim +0). Pokud jdeme zprava k bodu x = 3, tak je situace opacna a staci si prekontrolovat znamenko treba dosazenim 3,1 (musi to byt cislo hodne blizko 3) - polopaticke deleni -0. Muzeme dosazovat i do celeho zapisu funkce, pokud nam nejde jinak urcit znamenko
Ja vim, ze dosazovanim nedokazujeme celek, ale da se to pouzit jako jednoduchou pomucku, nez to clovek trochu zazije a ma nacviceno.
Jelikoz se to pak hodne vyuziva pri vysetreni prubehu funkce, je dobre si vytvorit nejakou podobnou pomucku.
Offline