Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » lineární funkcionál (TOTO TÉMA JE VYŘEŠENÉ)
#2 03. 02. 2012 18:41
Re: lineární funkcionál
Ahoj ↑ simonaj1:,
Si si ista ze  je spravne vypocitane?
je spravne vypocitane?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 03. 02. 2012 19:27 — Editoval vanok (03. 02. 2012 19:29)
Re: lineární funkcionál
Pokusim sa najprv vseobecne vyjasnit co moze znamenat pojem "suradnice funkcionalu"
Tak najprv trocha teorie: (iste ste to takto videli aj na prednaske)
Bud dana jedna basa priestoru  ,
, suradnice vektoru
suradnice vektoru  sa pisu vo forme stlpcoveho vektoru:
sa pisu vo forme stlpcoveho vektoru:
 .
.
A opacne , linearna forma alebo kovektor je representovany riadkovym vektorom z  suradnicamy :
suradnicamy :
 .
.
Takze mozme pisat vo forme vektoroveho sucinu:
 .
.
Od tialto je lahko posudit tvoju metodu.
V standardnej base tvoja linearna forma je dana vektorom 
a v novej baze je ???
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 03. 02. 2012 22:02
Re: lineární funkcionál
↑ simonaj1:,
Pomoc:
Obraz vektoru 
je

Obraz vektoru  je -4
je -4
ale podla toho co pises to nesedi!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 04. 02. 2012 08:25
Re: lineární funkcionál
tak teď z toho nejsem vůbec moudrá?! myslela jsem že budu mít: , ale pochopila jsem z tvé poslední "nápovědy", že to mám špatně.
, ale pochopila jsem z tvé poslední "nápovědy", že to mám špatně.
píšeš, že obraz vektoru  = -4, ale nechápu proč obrzem pro "trojku" je "jednička"
= -4, ale nechápu proč obrzem pro "trojku" je "jednička"
jeslti to chápu, kanonická baze jsou vektory 
 >>
>>  takže V_x pro kanonickou bazi je (4, -1, 1)
takže V_x pro kanonickou bazi je (4, -1, 1)
ale dál fakt nevím...
Offline
#8 04. 02. 2012 09:34 — Editoval vanok (04. 02. 2012 09:38)
Re: lineární funkcionál
Najprv 3 vseobecne poznamky:
1)Treba mat vzdy na mysli, ze obraz toho isteho vektoru aplikaciou f je vzdy ten isty (inac by f nebola dobre definovana)
2)Pouzitie roznych baz na napisanie jedneho vektoru, znamena, ze ho raz pises ako linearnu kombinaciu jednej alevo druhej bazy.
3)Obraz linearnej kombinacie vektorov, jednou linearnou applikaciou je "analogicka" linearna kombinacia obrazov vektorov.
V tvojom priklade to znamena:



lebo

co mozes vyjadrit aj takto
 je
je  obraz vektoru
obraz vektoru 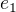 , standarnej bazy
, standarnej bazy je
je  obraz ...
obraz ...To preto mozes pisat ze

cize
 je kovektor
je kovektor  vo standardnej baze.
vo standardnej baze.A teraz musis urobit to iste z vektormy baze

Tak vdaka vsetkym poznamkach mas teraz ozaj vsetko na riesenie problemu
Treba najst

No to uz dokazes sama
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 04. 02. 2012 10:12
Re: lineární funkcionál
↑ simonaj1:
Nie.
Ako si to pocitala?
Prestuduj si este raz co som pisal.
Ake skripta pouzivas? Co studujes?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 04. 02. 2012 10:21
Re: lineární funkcionál
↑ vanok: žádná skripta, jen výpomoc kamarádce, která neumí s maticemi vůbec, naposled jsem tuhle matiku měla před 3 roky a tohle jsme tam neměli, takže vůbec nevím kudy do toho... bohužel jsem funkcionál ve skriptech, která mám nenašla (ČVUT), ani na netu nic z čeho bych byla moudřejší a zatím se topím i v tvém výkladu
Offline
#12 04. 02. 2012 10:41
Re: lineární funkcionál
↑ simonaj1:
takže ještě jeden pokus (0,13, -4)
počítala jsem
4*1 + (-1)*3 + 1*(-1) = 4-3-1 = 0 (předtím početní chyba)
4*3 + (-1)*(-1) + 1*0 = 12+1+0= 13
4*0 + (-1)*4 + 1*0 = 0-4+0 = -4
Offline
#13 04. 02. 2012 10:50
Re: lineární funkcionál
↑ simonaj1:,
Ano, potom nie je to jednoduche pre teba... ale asi by bolo lepsie, aby tvoja priatelka sama ukazala napr tu na fore, co su jej skutocne tazkosti.
Inac, co studujes, ja to volam linearna forma... v tomto presmon pripade.
Urcenie: 
Treba pouzit, ze  v standarnej baze.
v standarnej baze.
Tak mame jednoducho 
Podobne  a tak
a tak 
A na koniec  a tak
a tak 
Cize tvoj kovektor  v novej baze sa pise
v novej baze sa pise
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 04. 02. 2012 12:09
Re: lineární funkcionál
↑ simonaj1:,
Tak dobre pokracovanie v tvojich reviziach matematiky.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » lineární funkcionál (TOTO TÉMA JE VYŘEŠENÉ)





 a nic ine.. a pripominam ze bezne sa skalary pisu pred vektormy... cize na lavo
a nic ine.. a pripominam ze bezne sa skalary pisu pred vektormy... cize na lavo