Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 02. 2012 21:07
- Dale.Lenka

- Příspěvky: 70
- Reputace: 0
Integrál
Ahoj,
potřebovala bych poradit. Počítám integrál s pomocí cylindrických souřadnic, ale zasekla jsem se u toho, že neumim vypočítat neurčitý integrál
Už jsem zkoušela substituci, per partes, ale vždycky se někde zacyklim a nejde mi to dál ....
Předem dík za pomoc, Lenka
Offline
#4 03. 02. 2012 21:15
Re: Integrál
↑ Dale.Lenka:
Vidis, co by se dalo delat dal? Ty jsi ten per partes asi zkousela predtim obracene?
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#5 03. 02. 2012 21:25
- Dale.Lenka

- Příspěvky: 70
- Reputace: 0
Re: Integrál
↑ Phate:
už jsem to zkoušela ze všech stran, dokonce i verze, o kterých jsem už od začátku tušila, že to tak nepůjde ...
teď mě ještě napadla snad už poslední ....  =
=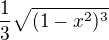
mám to dobře?
Offline
#6 03. 02. 2012 21:25 — Editoval Rumburak (03. 02. 2012 21:31)
Re: Integrál
↑ Dale.Lenka:
A co ta substituce ? Kterou jsi zkoušela ? Já bych navrhoval 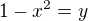 , takže
, takže
EDIT. Pokud jde o kontrolu Tvého výsledku: mně navrženou metodou vyšetl výsledek stejný až na znaménko.
Offline
#7 03. 02. 2012 21:28
- Dale.Lenka

- Příspěvky: 70
- Reputace: 0
Re: Integrál
↑ Rumburak:
proč je tam to minus?
mě substituce vyšla  a z toho
a z toho 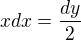
Offline
#8 03. 02. 2012 21:30
- Dale.Lenka

- Příspěvky: 70
- Reputace: 0
Re: Integrál
[re]p258517|Dale.Lenka[/re
už to vidím ....
Offline
#9 03. 02. 2012 21:36
- Dale.Lenka

- Příspěvky: 70
- Reputace: 0
Re: Integrál
díky moc ... konečně mi vyšel výsledek ... teď už jen ten samý příklad vypočítat ve sférických ....
Offline
#11 05. 02. 2012 12:40
- Dale.Lenka

- Příspěvky: 70
- Reputace: 0
Re: Integrál
↑ Phate:
to jsem se právě zacyklila a dál to nešlo ...
Offline

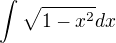 ?
?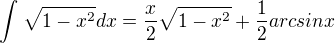
 .
.