Matematické Fórum

check_drummer

Ahoj,
mějme těleso T. Patí potom následující tvrzení?:

Existuje-li pro každý prvek t z T a každé k přirozené, prvek d z T takový, že 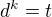$d^k=t$ , tak potom je T algebraicky uzavřené (tj. každý polynom s koeficienty v T má kořen z T).

Platí toto tvrzení i tehdy (tedy pokud opravdu platí), pokud nepožadujeme platnost tvrzení pro všechna k, ale jen pro k=2?

Edit: Rovněž by bylo zajímavé zkoumat, zda platí obrácené tvrzení (tj. že z uzavřenosti plyne existence onoho prvku d).

Děkuji

FailED · 05. 02. 2012 23:32 — Editoval FailED (06. 02. 2012 01:53)

Zdravím,

Autor skryl část textu. Zobrazit/skrýt!

check_drummer · 07. 02. 2012 21:03

Ahoj, děkuji za odpověď. Nerozumím však tomu, jak ze skrytého faktu plyne, že Tebou uvedený polynom nemá kořeny.

FailED napsal(a):
Autor skryl část textu. Zobrazit/skrýt!
Skrytý text:

pro $d\neq 0$ musí být aspoň jeden z prvků $d, d^2, d^3,\ldots ,d^{|T|-1}$ jedna.

Díky za vysvětlení.

vanok · 07. 02. 2012 21:28 — Editoval vanok (07. 02. 2012 21:29)

Ahoj ↑ check_drummer:,
len mala poznamka:
Pises:
Existuje-li pro každý prvek t z T a každé k přirozené, prvek d z T takový, že 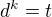$d^k=t$ , tak potom je T algebraicky uzavřené (tj. každý polynom s koeficienty v T má kořen z T).

Toto je nemozne v pripade konecneho telesa.
Podobny agrument ako dal kolega ↑ FailED::
dva prvky musia byt v tejto postupnosti
$d, d^2, d^3,\ldots ,d^{|T|}$
rovnake...( mame $|T|-1$ nenulovych prvkov, tak vdaka Dirichlet-ovemu principu mame 2 rovnake prvky v pozstupnosti)
To znamena, ze $d^i=d^j$ pre dva rozne i a j ak napr $i>j$ , mame $d^{i-j}=1$
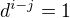
ale zaroven predpokladas s $d^{i-j}= t$ ...a to je protiklad.

FailED · 07. 02. 2012 21:31

↑ check_drummer:

Autor skryl část textu. Zobrazit/skrýt!

check_drummer · 07. 02. 2012 21:57

↑ FailED:↑ vanok:
Ahoj, děkuji za objasnění.
Abych řekl pravdu, spíš mě k formulaci tohoto tvrzení motivovala nekonečná tělesa. Jak píše kolega ↑ FailED:, znamenala by platnost tohoto tvrzení i platnost základní věty algebry, což jsem si při formulaci také uvědomil (vlastně to byla jedna z hlavních motivací této formulace). Ale jde o relativně obecné tvrzení, tak je otázka, zda bude aspoň pro nekonečná tělesa pravdivé.

Vlastně, když o tom tak přemýším, tak tvrzení říká: Má-li každý polynom tvaru $x^k-t$ kořen v T, pak má každý polynom kořen v T. Jistá zajímavost v tom je. :-)

check_drummer · 08. 02. 2012 19:13

↑ FailED:↑ vanok:
Když o tom tak přemýšlím, tak jste vlastně větu pro konečný případ nikoli vyvrátili, ale dokázali - ukázali jste totiž, že předpoklady nejsou nikdy splněny. :-)

FailED · 08. 02. 2012 19:43 — Editoval FailED (08. 02. 2012 19:48)

↑ check_drummer:

Ukázalo se, že předpoklady nemůžou být splněny v konečném případě, v nekonečném už Dirichletův prnicip nefunguje.

V každém algebraickém tělese (třeba $\mathbb{C}$ ) je podmínka splněna - pro daná k, t je kořen polynomu $x^k-t$ právě hledané d.

Matematické Fórum

#1 05. 02. 2012 15:47 — Editoval check_drummer (05. 02. 2012 16:43)

Algebraicky uzavřené těleso a vyjádření každého prvku jako mocnina

#2 05. 02. 2012 23:32 — Editoval FailED (06. 02. 2012 01:53)

Re: Algebraicky uzavřené těleso a vyjádření každého prvku jako mocnina

#3 07. 02. 2012 21:03

Re: Algebraicky uzavřené těleso a vyjádření každého prvku jako mocnina

FailED napsal(a):

#4 07. 02. 2012 21:28 — Editoval vanok (07. 02. 2012 21:29)

Re: Algebraicky uzavřené těleso a vyjádření každého prvku jako mocnina

#5 07. 02. 2012 21:31

Re: Algebraicky uzavřené těleso a vyjádření každého prvku jako mocnina

#6 07. 02. 2012 21:57

Re: Algebraicky uzavřené těleso a vyjádření každého prvku jako mocnina

#7 08. 02. 2012 19:13

Re: Algebraicky uzavřené těleso a vyjádření každého prvku jako mocnina

#8 08. 02. 2012 19:43 — Editoval FailED (08. 02. 2012 19:48)

Re: Algebraicky uzavřené těleso a vyjádření každého prvku jako mocnina

Zápatí