Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 02. 2012 18:33 — Editoval FlyingMonkey (07. 02. 2012 18:44)
- FlyingMonkey

- Příspěvky: 758
- Reputace: 4
Vektory - lineární kombinace?
Ahoj :)
Chci se zeptat ohledně vektorů - lineární kombinace, k čemu je to dobré?
máme si zopakovat obecně vektory a tohle tam je, nikde na to nemůžu najít žádný materiál ..
našel jsem jeden příklad, který byl ve VŠ sekci, podle toho jse mto zkusil:
"Vektor z = (2;-2;-10) zapište jako lineární kombinaci vektorů u,v,w kde u=(2;1;-1) v =(2;3;2),
w(4;5;-2)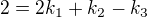
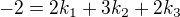
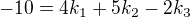
Gausovkou se mi po zachování druhé a odečtení od toho 1. a 2. rovnice dostane ale divného výsledku: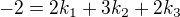
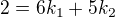
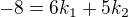
Co s tím v tuhle chvíli? Dík )
EDIT:
našel jsem si, že mám pravděpodobně špatně zápis té soustavy, takže to vyzkouším a dám vědět, díky :)
Offline
- (téma jako vyřešené označil(a) FlyingMonkey)
#2 07. 02. 2012 22:12
Re: Vektory - lineární kombinace?
Lineární kombinace je jediná věc, kterou můžeš s vektorama dělat!
Vektorový prostor je množina, kde můžes prvky(=vektory) sčítat a násobit skalárem, ale to je všechno.
Netuším, co všechno víš, ale: když máš množinu vektorů tvořící bázi, tak se dá libovolnej vektor zapsat jako lineární kombinace bazových vektorů. Například když máš dva vektorové prostory, tak lineární funce mezi nima je plně určena efektem na bázové vektory, protože každý vektor se dá vyjádřit jako lineární kombinace báze a lineární funkce respektuje lineání kombinace.
Offline