Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 10. 02. 2012 13:38
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Integrály
Ono je to opravdu v podstate to same, jenom se rovnost pouziva jednou z jedne a jednou z druhe strany.
Pro hlubsi diskusi doporucuji opsat, co presne o tom mate ve skriptech.
Offline
#5 10. 02. 2012 15:57
Re: Integrály
↑ kaja.marik:
Tak ve skriptech je první substituční metoda definovaná jako: Nechť fce f má primitivní fci F na otevřeném intervalu J. Nechť funkce \varphi zobrazuje otevřený interval I do J a má na intervalu I konečnou derivaci. Potom F ^\circ \varphi (složená fce) je primitivní fcí k funkci (f^\circ \varphi ) \varphi^{-1} na intervalu I a platí
\int_{}^{} f( \varphi (t)) \varphi ´(t)dt=F( \varphi (t))+c, c leží v \mathbb{R} .
A ta druhá substituční metoda je: Nechť funkce \varphi zobrazuje otevřený ionterval I na intervalu J a nechť má konečnou derivaci \varphi ´se nerovná 0 na I. Je-li G primitivní k funkci (f° \varphi ) \varphi ´ na I, pak funkce G° \varphi ^{-1} je primitivní k f na J a platí
\int_{}^{} f(x)dx=\int_{}^{} f( \varphi (t)) \varphi ´(t)dt=G(t)+c=G( \varphi ^{-1} (x))+ c
↑ Rumburak:
Na to jsem se dívala než jsem sem psala, ale i tak jsem to nepochopila.
Offline
#7 10. 02. 2012 16:01
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Integrály
Neco jako http://user.mendelu.cz/marik/mat-web/mat-webse9.html , vety 1.6 a 1.7 ?
Offline
#9 10. 02. 2012 17:06
Re: Integrály
↑ aralk09:
Výpočet podle vzorce
(1) 
můžeme provádět buďto ve směru zleva doprava nebo zprava doleva podle toho, kterou stranu vzorce umíme určit (resp. spočítat).
Umíme-li určit integrál na pravé straně, můžeme vzorec použít k výpočtu levé strany.
Umíme-li určitt integrál na levé straně, můžeme vzorec použít k výpočtu pravé strany.
Druhou věcí je pochopit důkaz, že vzorec (1) platí - odvozuje se z věty o derivaci složené funkce .
Offline
#10 11. 02. 2012 13:32
Re: Integrály
↑ Rumburak:
Takže ta první metoda je, že když integruju nějakou fci, tak za t dosazuju "kus" té fce a to derivuji a ta druhá substituční metoda je, že za t dosazuju něco tak aby, když to zderivuju vyšlo "kus" té fce? Chápu to dobře?
Offline
#11 13. 02. 2012 11:26 — Editoval Rumburak (13. 02. 2012 13:55)
Re: Integrály
↑ aralk09:
Snad to myslíš správně, ale popisuješ to příliš vágně, než aby to stačilo k jednoznačné odpovědi ANO resp. NE. Popisovat složitější matematické souvislosti
hovorovým jazykem je ošidné, což řešíme matematickou terminologií a symbolikou. Navíc mi činí potíže pamatovat si, která z vět o substituci je "první"
a která "druhá" :-( (protože nikdy jsem to nepotřeboval vědět).
Ukáži další příklady:
A) Máme spočítat  . Substititucí
. Substititucí  (a tedy
(a tedy  ) získáme "tabulkový" integrál:
) získáme "tabulkový" integrál:
 .
.
B) Máme spočítat strašidelně vyhlížející integrál  na intervalu
na intervalu 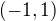 . Substitituce
. Substitituce  (tj.
(tj.  )
)
pro  nám ho převede na integrál
nám ho převede na integrál
 .
.
V obou těchto příkladech A), B) byla použita tatáž substituce  , avšak dvěma různými způsoby, což jsou právě ony dvě varianty věty o substituci.
, avšak dvěma různými způsoby, což jsou právě ony dvě varianty věty o substituci.
PS. Substituci z příkladu B) lze s úspěchem pojmout i obráceně - v duchu příkladu A) - díky tomu, že funkce sinus ja na uvažovaném intervalu  prostá:
prostá:
 zde znamená
zde znamená  , takže
, takže  a
a
 .
.
Offline
