Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 02. 2012 11:56
Derivace "e"
Zdravím,
měl jsem teď u zkoušky příklad, který jsem trochu zkazil, protože mi nedošlo, jak derivovat. Mějme funkci
Máme dokázat, že tato funkce se pro žádné x > 0 nerovná číslu e či 0 (nepamatuji si, co z toho to bylo, ale jestli se nepletu, tak bych svým způsobem měl dokázat oboje).
Dospěl jsem k tomu, že jsem si udělal limity v nule a v plus nekonečnu a pak jsem chtěl dokázat, že funkce je ryze monotónní,
Tedy 

Následně jsem chtěl funkci pro  zderivovat, ale došel jsem k tomu, že nevím, jak takovou funkci zderivovat, což je asi ostuda.
zderivovat, ale došel jsem k tomu, že nevím, jak takovou funkci zderivovat, což je asi ostuda.
Jimmy
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#3 13. 02. 2012 12:41
Re: Derivace "e"
↑ Alkac:
Takže dostanu tohle?
Moc ale nevím, co z toho dostanu... A taky bych se rád zbavil logaritmu a  , ale netuším v tuhle chvíli, jak bych to provedl. Ta derivace vychází pěkně hnusně, jak z toho určím, že funkce je na celém Df rostoucí?
, ale netuším v tuhle chvíli, jak bych to provedl. Ta derivace vychází pěkně hnusně, jak z toho určím, že funkce je na celém Df rostoucí?
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#4 13. 02. 2012 13:04
Re: Derivace "e"
Ted uz se s tim musis proste poprat, nikdo nesliboval ze ta derivace vyjde hezky:)
Ty chces aby tohle bylo vetsi nez nula pro x vetsi nez nula. Ten prvni clen e^(...) je vetsi nez nula, takze tim tu nerovnost muzes vydelit. Pak zbude ln(1+x) - 1/(x+1)>0 jestli to dobre vidim a potom bych pouzival neco takovyho http://functions.wolfram.com/Elementary … g/29/0001/
Je to jenom napad, nepocital jsem to
Offline
#5 13. 02. 2012 13:08 — Editoval vanok (13. 02. 2012 14:10)
Re: Derivace "e"
Ahoj ↑ found:,
Podla mna treba staci vysetrit zakladne vlasnosti tvojej funkcie.
Najrv vysetri obor definicie, a najdi limity v hranicnych bodoch.
Najdes medzi inym, ze limita v je
je  .
.
A limity na lavo a na pravo bodu
 ( ak existuju) ti daju dalsie dolezite (pre teba ) informacie
( ak existuju) ti daju dalsie dolezite (pre teba ) informacie.... a
vdaka vypoctu 1vej derivacie a studiu jej znamienka, dostanes informacie o monotonii tvojej funkcii...A zvysok je ozaj jednoduchy.
Poznamka 1: na tvoju otazku o
 stacia neskryte informacie...i ked tie ine ti pomozu lepsie vizualizovat o co ide.
stacia neskryte informacie...i ked tie ine ti pomozu lepsie vizualizovat o co ide.Poznamka 2: je utopocke dufat, ze nejaka funkcia co ma vertikalnu asymptotu bude "striktne" monotona, to moze byt len na konexnych intervaloch.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 13. 02. 2012 13:18 — Editoval Honzc (13. 02. 2012 13:34)
Re: Derivace "e"
↑ found:
Už jsem to tady několikrát propagoval:
"logaritmická" derivace.
Tedy:
Funkce typu  jednoduše "zlogaritmujeme" a máme:
jednoduše "zlogaritmujeme" a máme:
Teď obě strany derivujeme
levou takto: (jako složenou funkci) 
pravou jako souučin:
a tedy 
Takže logaritmu se nezbavíš, ale e ano.
Offline
#7 13. 02. 2012 13:50
Re: Derivace "e"
Logaritmicka derivace je dobra rada, poprve jsem to videl v jedne knize o analyze (ale na nazev si nemuzu vzpomenout) a nektere priklady se tim daji vyresit opravdu efektne. Tady to jeste neni tak videt, ale obcas je to opravdu k nezaplaceni
Offline

 je vodorovna ( horizontalna ) asymptota gra tvojej funkcie
je vodorovna ( horizontalna ) asymptota gra tvojej funkcie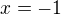 je rovnica jedinej zvyslej (vertikalnej) asymptoty grafu tvojej funkcie)...
je rovnica jedinej zvyslej (vertikalnej) asymptoty grafu tvojej funkcie)... 