Matematické Fórum

UnknownDeletedUser

-

Alkac · 14. 02. 2012 00:59

Myslim ze to tady velice nedavno bylo

Mihulik · 14. 02. 2012 08:28

Ahoj,
zkus důkaz sporem. Nechť existuje těleso t.ž. 0=-1 a pomocí axiomů tělesa po několika úpravách dostaneš, že 1=0.:)

jelena · 14. 02. 2012 09:23

Zdravím,

ještě přidám jeden odkaz, kde bylo řešeno, ale mám dojem, že bylo ještě jedno téma. ↑ Alkac: je to ono nebo ještě jiné téma? Děkuji.

vanok · 14. 02. 2012 09:24

ahoj,

Jedna definicia telesa je takto formulovana:

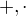Mnozina $K$ z 2mi zakonmy $+,\cdot$ je teleso ak:
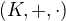* $(K,+,\cdot)$ je okruh
* $0_{K}\neq1_{K}$
* Vsetki prvky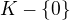 $K-\lbrace 0\rbrace$ maju inverzny prvok pre $\cdot$ v $K$

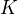
Ak ste ju inac formuloli, mozes dokazat ze ta vasa je equivalentna z tvojov.