Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Neurčitý integrál (per partes) (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 02. 2012 11:35
Neurčitý integrál (per partes)
Ahoj,
řeším následující neurčtý integrál pro všechna 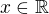 .
.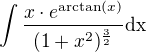
V zadání je napsáno, že by měl jít nejsnáze řešit pomocí metody per partes, ale pokaždé, když jsem ji zkusil použít pro nějakou volbu 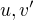 , tak se integrál ještě více zesložitil. Nemáte nějaký tip?
, tak se integrál ještě více zesložitil. Nemáte nějaký tip?
Děkuji.
Offline
- (téma jako vyřešené označil(a) Sulfan)
#3 25. 02. 2012 11:55 — Editoval Sulfan (25. 02. 2012 12:00)
Re: Neurčitý integrál (per partes)
↑ jardofpr:
To znamená druhá věta o substutici?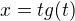
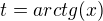
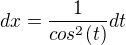
To dá integrál 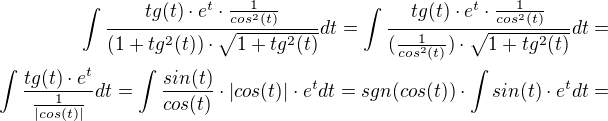
Teď per partes a je hotovo?
Offline
#6 25. 02. 2012 12:05 — Editoval jardofpr (25. 02. 2012 12:19)
Re: Neurčitý integrál (per partes)
↑ Sulfan:
no výsledok by mal byť dobre
ale ten prvý zlomok máš aj tak zbytočne zložitý
teda chcem tým povedať že by asi bolo lepšie 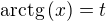
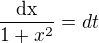
z toho rovno vylezie iba 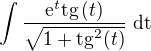
pravdupovediac ma trochu trapi na tom nespojitost vyslednej funkcie
ked tak na to pozeram
funkcia v zadani je spojita vsade, zda sa mi blbost aby mala nespojitu primitivnu funkciu
to bude chciet inu cestu
ono ta tangensova substitucia totiz rozdeli definicny obor na intervaly dlzky pi, a v krajnych bodoch to moze potom uletiet, na to sme nejak nepomysleli
predsa to bude chciet inu cestu zrejme
minimalne spojitu substituciu nejaku ked tak
Offline
#7 25. 02. 2012 12:20 — Editoval Sulfan (25. 02. 2012 12:21)
Re: Neurčitý integrál (per partes)
↑ jardofpr: aha, ušetřil bych jeden krok, to je pravda. Nicméně tedy bych dál po provedení per partes na 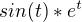 pokračoval na:
pokračoval na: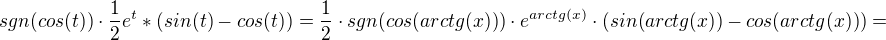

edit: Výsledná funkce je všude spojítá, kde by mohl být zádrhel?
Offline
#8 25. 02. 2012 12:33 — Editoval jardofpr (25. 02. 2012 12:35)
Re: Neurčitý integrál (per partes)
↑ Sulfan:
teoreticky tam zádrhel je
substitúcia čo sme spravili obmedzila  o body
o body 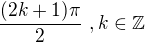
pre ne sme ďalšie úpravy robiť nemohli, tým padom funkcia ktorú sme našli je primitívnou ku funkcii pod integrálom na interevaloch rovnakej dĺžky,
teoreticky nezáleží na tom či je spojitá alebo nie lebo už od tej substitúcie v tých bodoch nie je definovaná
Offline
#9 25. 02. 2012 12:35 — Editoval Sulfan (25. 02. 2012 12:36)
Re: Neurčitý integrál (per partes)
↑ jardofpr: Ale zároveň, když v těchto bodech spočítáme limitu primitivní funkce zprava i zleva, tak se rovnají, tudíž funkční hodnotu v takovém bodě můžeme dodefinovat jako hodnotu této limity (což není nutné, protože jde o přímo funkční hodnotu). Nebo ne?
Offline
#10 25. 02. 2012 12:38 — Editoval jardofpr (25. 02. 2012 12:41)
Re: Neurčitý integrál (per partes)
↑ Sulfan:
to máš pravdu, tá funkcia je primitívna k podintegrálnej na celom  ,
,
len vravím že sme ju týmto na celom  nenašli
nenašli
v tomto prípade je to ok, dá sa to vyriešiť ako si povedal
ale vo všeobecnosti to úplne korektné zrejme nebude, len tolko som chcel povedať :)
každopádne výsledok je správny
inak per partes by bol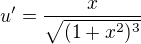
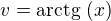
Offline
#11 25. 02. 2012 12:41
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Neurčitý integrál (per partes) (TOTO TÉMA JE VYŘEŠENÉ)

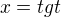 ?
?