Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 01. 03. 2012 09:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nejmenší obsah
↑↑ Cheop:
Také pozdrav :-)
neotevřu ani náhodou. Kolegové mají zájem svůj problém vyřešit, podpoříme samostatnou práci, prosím.
Další OT příspěvky budu mazat, téma pro debaty jsem již odkázala. Děkuji.
Offline
#27 01. 03. 2012 09:46
Re: Nejmenší obsah
↑↑ jelena:
No jo, tak to byla ode me uplna blbost, ze jsem prehledl, ze q vyjadruju uplne spatne. Uz jsem to opravil. A potom jsem zkusil dosadit to vyjadrene q do rovnice  , kde za kazde k dosadim
, kde za kazde k dosadim 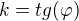 , coz dela
, coz dela 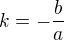 a vyjde mi vysledek
a vyjde mi vysledek 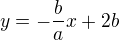 , coz by mel byt spravny vysledek.
, coz by mel byt spravny vysledek.
Ted to jeste zkusim dopocitat tim Vasim zpusobem, protoze by me zajimalo, jestli to vyjde taky. Jenom by me zajimalo, jak bych mohl obhajit, ze prave pro tento vysledek bude S ten nejmensi. V tom mi ma pomoct ta derivace, nemylim-li se?
1 + 1 = 2
Offline
#28 01. 03. 2012 09:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nejmenší obsah
↑ 2rec:
nemíchej, prosím všechno dohromady. Nejdřív projdi jedno řešení (můj postup je standardní), potom alternativy (Tvé :-)
Proto jsem upozorňovala na pořádek v označení - souřadnice bodu A(a,b) je něco jiného, než 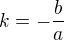 , tudy nepůjdeme.
, tudy nepůjdeme.
Obhajovat budeme také standardně - derivace sestavené funkce S=f(k)
Offline
#30 01. 03. 2012 10:25
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nejmenší obsah
↑ 2rec:
No vidíš. Děkuji, je to skoro dobře, ještě jednou překontroluj, jak jsi vyjadřoval (není to úplně OK). Např. pro P_x máme:
y=0, potom  , odsud x=...
, odsud x=...
Stejně i pro P_y x=0, potom 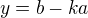 . Až překontroluješ, skutečně dosadíme do S souřadnice, jak jsi napsal.
. Až překontroluješ, skutečně dosadíme do S souřadnice, jak jsi napsal.
Offline
#40 01. 03. 2012 11:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nejmenší obsah
↑ 2rec:
všechno v pořádku, máš 2 různé přímky, procházející zadaným bodem A. Pouze jedna přímka však společně s osou Ox, Oy vytvaří nedegenerovaný trojúhelník v 1. kvadrantu - která a proč?
Svůj výsledek q=2b (psal jsi v některém příspěvku) tedy máš i "oficiální" cestou. Teď už si prosím, porad, dlouho nebudu v dosahu. Ať se vede.
Offline
#41 01. 03. 2012 12:29
Re: Nejmenší obsah
↑ jelena:
Tak uz vim :) q se nesmi rovnat 0, jinak by primka prochazela pocatkem soustavy souradnic.
Priklad je tedy hotovy. Mockrat dekuju, hodne jsem se naucil a slibuju, ze jestli sem budu jeste nekdy neco psat, budu radsi merit (kontrolovat) ne 2x, ale rovnou 3x, nez zacnu rezat (psat).
1 + 1 = 2
Offline
#42 01. 03. 2012 23:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Nejmenší obsah
↑ 2rec:
není za co, také děkuji za samostatnou snahu (a také kolegům v tématu). Řešení od kolegy Honzce jsem poslala Tobě přes PM. Kolegovi děkuji a ještě jednou omluva za skrytí hotového řešení.
Téma označím za vyřešené - do příštího ročníku :-)
Offline

![kopírovat do textarea $P_x = [\frac{b-ka}{k}; 0] , P_y = [0; ka - b]$](/mathtex/57/57222713d9e53661b37d38219e3059cc.gif) . Ted uz mam snad posledni otazku. Mam dosadit do vzorce
. Ted uz mam snad posledni otazku. Mam dosadit do vzorce 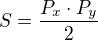 , za P_x dosadim xovou souradnici P_x a za P_y dosadim yovou souradnici P_y?
, za P_x dosadim xovou souradnici P_x a za P_y dosadim yovou souradnici P_y?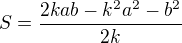 . Ted to jdu zderivovat.
. Ted to jdu zderivovat.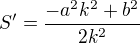 . Pro jistotu to jeste zkontroluju a pak zkusim ty extremy.
. Pro jistotu to jeste zkontroluju a pak zkusim ty extremy.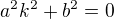 , coz bez komplexnich cisel nevyjde.
, coz bez komplexnich cisel nevyjde.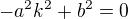
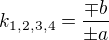
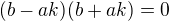
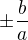 . To jsem ted dosadil oboje do puvodni rovnice spolu s y=b a x=a a vysledky jsou
. To jsem ted dosadil oboje do puvodni rovnice spolu s y=b a x=a a vysledky jsou 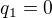 a
a 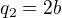 .
.