Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Říjnový nevlastní integrál (konvergence) (TOTO TÉMA JE VYŘEŠENÉ)
#2 12. 10. 2008 02:44 — Editoval Pavel (12. 10. 2008 17:18)
Re: Říjnový nevlastní integrál (konvergence)
Podařilo se mi dokázat, že bude-li  , bude integrál divergentní. Je zřejmé, že aby měly výrazy pod odmocninami smysl, musí platit
, bude integrál divergentní. Je zřejmé, že aby měly výrazy pod odmocninami smysl, musí platit  a
a  . Případ
. Případ 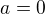 a
a 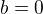 je triviální. Nech? je alespoň jedna z konstant a, b různá od 0.
je triviální. Nech? je alespoň jedna z konstant a, b různá od 0.
Použijme Lagrangeovu větu o střední hodnotě:
![kopírovat do textarea $\Large\sqrt{\sqrt{x+a}-\sqrt{x}}\,>\,\sqrt{\frac a2}\,\cdot\,\frac 1{\sqrt[4]{x+a}} $](/mathtex/6e/6ea761d4232d15ac96d0b6db62bf639a.gif)
![kopírovat do textarea $ \frac{\sqrt{x}-\sqrt{x-b}}{x-(x-b)}=\frac 1{2\sqrt{\eta}}\,\qquad\eta\in(x-b,x)\nl \sqrt{x}-\sqrt{x-b}=\frac b2\,\cdot\,\frac 1{\sqrt{\eta}}\,<\,\frac b2\,\cdot\,\frac 1{\sqrt{x-b}}\nl \sqrt{\sqrt{x}-\sqrt{x-b}}\,<\,\sqrt{\frac b2}\,\cdot\,\frac 1{\sqrt[4]{x-b}} $](/mathtex/d0/d082061ca7ad9f0848252c70045748ef.gif)
![kopírovat do textarea $ \Large -\sqrt{\sqrt{x}-\sqrt{x-b}}\,>\,-\sqrt{\frac b2}\,\cdot\,\frac 1{\sqrt[4]{x-b}} $](/mathtex/a3/a3ef541ef44bbfcadc50cb1a434f66ba.gif)
Původní integrál mohu nahradit tímto:![kopírovat do textarea $ \left|\int_{b}^{\infty}\left (\sqrt{\sqrt{x+a}-\sqrt{x}}-\sqrt{\sqrt{x}-\sqrt{x-b}}\right )\,\rm{d}x\right|\,>\,\left|\int_{b}^{\infty}\left (\sqrt{\frac a2}\,\cdot\,\frac 1{\sqrt[4]{x+a}}-\sqrt{\frac b2}\,\cdot\,\frac 1{\sqrt[4]{x-b}}\right )\,\rm{d}x\right|=\frac 43\left|\,\left[\sqrt{\frac a2}\,\cdot\,\sqrt[4]{(x+a)^3}-\sqrt{\frac b2}\,\cdot\,\sqrt[4]{(x-b)^3}\right]_b^{\infty}\right| $](/mathtex/f8/f84b9f55cbe6c810497395693b79a42f.gif)
Nyní stačí spočítat limitu primitivní funkce v  . Původní integrál je divergentní, je-li limita nevlastní.
. Původní integrál je divergentní, je-li limita nevlastní.![kopírovat do textarea $ \lim_{x\to\infty}\left|\sqrt{\frac a2}\,\cdot\,\sqrt[4]{(x+a)^3}-\sqrt{\frac b2}\,\cdot\,\sqrt[4]{(x-b)^3}\right|=\lim_{x\to\infty}\left|\sqrt[4]{\frac{a^2}{4}\,(x+a)^3}-\sqrt[4]{\frac{b^2}{4}\,(x-b)^3}\right|=\nl=\lim_{x\to\infty}\left|\frac{\frac{a^2}{4}\,(x+a)^3-\frac{b^2}{4}\,(x-b)^3}{\sqrt[4]{\left(\frac{a^2}{4}\,(x+a)^3\right)^3}+\sqrt[4]{\left(\frac{a^2}{4}\,(x+a)^3\right)^2\left(\frac{b^2}{4}\,(x-b)^3\right)}+\sqrt[4]{\left(\frac{a^2}{4}\,(x+a)^3\right)\left(\frac{b^2}{4}\,(x-b)^3\right)^2}+\sqrt[4]{\left(\frac{b^2}{4}\,(x-b)^3\right)^3}}\right|=\nl= \lim_{x\to\infty}\left|\frac{x^3(\frac{a^2}{4}-\frac{b^2}{4})+x^2(\frac{3a^3}{4}+\frac{3b^3}{4})+x(\frac{3a^4}{4}-\frac{3b^4}{4})+\frac{a^5}{4}+\frac{b^5}{4}}{x^{\frac 94}\left[\sqrt[4]{\left(\frac{a^2}{4}\,(1+\frac ax)^3\right)^3}+\sqrt[4]{\left(\frac{a^2}{4}\,(1+\frac ax)^3\right)^2\left(\frac{b^2}{4}\,(1-\frac bx)^3\right)}+\sqrt[4]{\left(\frac{a^2}{4}\,(1+\frac ax)^3\right)\left(\frac{b^2}{4}\,(1-\frac bx)^3\right)^2}+\sqrt[4]{\left(\frac{b^2}{4}\,(1-\frac bx)^3\right)^3}\right]}\right|=\nl= \lim_{x\to\infty}\left|\frac{x^3(\frac{a^2}{4}-\frac{b^2}{4})}{Kx^{\frac 94}}\right|=\left|\frac{\frac{a^2}{4}-\frac{b^2}{4}}{K}\right|\lim_{x\to\infty}\left|x^{\frac 34}\right|, $](/mathtex/36/362f4b8d93ab09e45af13336cbc2ffa5.gif)
kde  je nějaká kladná reálná konstanta nezávislá na
je nějaká kladná reálná konstanta nezávislá na  . Limita bude nevlastní, jestliže
. Limita bude nevlastní, jestliže 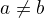 .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 12. 10. 2008 17:59 — Editoval BrozekP (12. 10. 2008 18:00)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Říjnový nevlastní integrál (konvergence)
Offline
#4 12. 10. 2008 19:28
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Říjnový nevlastní integrál (konvergence)
Zbývá spočítat 
Podle Mathematica to jde, řekl bych, že výsledek je celkem hezký :-)
Offline
#5 12. 10. 2008 22:00 — Editoval Marian (12. 10. 2008 22:04)
Re: Říjnový nevlastní integrál (konvergence)
↑ Pavel:↑ BrozekP:
Zdravím oba! Věděl jsem, že vás dva tahle úloha nenechá v klidu. Dá se uvažovat i následující postup (předpokládám již, že čísla a a b jsou kladná):
podobně
Odtud snadno
Druhý integrál je ale jasně konvergentní. Tedy divergence/konvergence původního integrálu je zřejmá z divergence/konvergence integrálu  . A tady je již diskuze snadná.
. A tady je již diskuze snadná.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Říjnový nevlastní integrál (konvergence) (TOTO TÉMA JE VYŘEŠENÉ)


![kopírovat do textarea $\|\int_{a}^{\infty}\frac{1}{\(\sqrt{x^2-a^2}+x\)\(\sqrt{x+a}+\sqrt{x-a}+2\sqrt{x}\)\(\sqrt{\sqrt{x+a}-\sqrt{x}}+\sqrt{\sqrt{x}-\sqrt{x-a}}\)}\,\mathrm{d}x\| \leq\|\int_{a}^{\infty}\frac{1}{x\cdot2\sqrt{x}\cdot\(\sqrt{\sqrt{x+a}-\sqrt{x}}\)}\,\mathrm{d}x\| =\|\int_{a}^{\infty}\frac{1}{x\cdot2\sqrt{x}\cdot\sqrt{\frac{a}{\sqrt{x+a}+\sqrt{x}}}}\,\mathrm{d}x\|\leq\nl \leq\|\int_{a}^{\infty}\frac{1}{x\cdot2\sqrt{x}\cdot\sqrt{\frac{a}{2\sqrt{x+a}}}}\,\mathrm{d}x\| =\frac{\sqrt2}{2\sqrt a}\|\int_{a}^{\infty}\frac{\sqrt[4]{x+a}}{x^{\frac32}}\,\mathrm{d}x\| \leq\frac{\sqrt2}{2\sqrt a}\|\int_{a}^{\infty}\frac{\sqrt[4]{2x}}{x^{\frac32}}\,\mathrm{d}x\| =\frac{\sqrt[4]{2^3}}{2\sqrt a}\|\int_{a}^{\infty}x^{\frac14-\frac32}\,\mathrm{d}x\| =\frac{\sqrt[4]{2^3}}{2\sqrt a}\|\int_{a}^{\infty}x^{-\frac54}\,\mathrm{d}x\|<+\infty$](/mathtex/75/759120b411e13ffab8c6a50f822e98c0.gif)