Matematické Fórum

myrek · 13. 03. 2012 00:10

jak se pomoci Taylora spocte taka limita $\lim_{n \to \infty}\frac{1}{\sqrt n}+ln(\sqrt{1+\frac 1n}-\frac{1}{\sqrt n})$
je mi jasne ze se to prevede do nuly ale co pak s tim logaritmem dyt znam rozvoje pro ln(1+n) a jak to tam napasovat?
dekuji moc

jardofpr

↑ myrek:

Taylor sa zdá byť zbytočná komplikácia, limita je pomerne očividná nula
ak to potrebuješ našiť na Taylora, snaž sa upraviť výraz v argumente logaritmu tak, aby sa tá jednotka vytvorila

myrek · 13. 03. 2012 00:41

↑ jardofpr:
no prave ze v zadani je napsane ze to musi byt dle Taylora

jardofpr

↑ myrek:

môžeš skúsiť výraz v argumente logaritmu upraviť nejak podobne ako toto

$\sqrt{1+\frac{1}{n}}-\frac{1}{\sqrt{n}}=\sqrt{\frac{n+1}{n}}-\frac{1}{\sqrt{n}}=\frac{\sqrt{n+1}-1}{\sqrt{n}}=1+\frac{\sqrt{n+1}-1}{\sqrt{n}}-1=1+\frac{\sqrt{n+1}-1-\sqrt{n}}{\sqrt{n}}$

aj keď neviem či sa to bude počítať dobre, ide len o to "umelé vytvorenie jednotky" ..

vanok · 13. 03. 2012 00:59 — Editoval vanok (13. 03. 2012 01:04)

↑ myrek:
Ak to mas povinne pocitat podla Taylor-oveho rozvoju
tak pocitaj postupne rozvoje
$R_1=\sqrt{1+\frac 1n}$ ( dva prve cleny stacia)
potom
$R_2=\ln (R_1-\frac{1}{\sqrt n})$ ( tu tiez dva prve cleny stacia)
a na koniec
$R_3=\frac{1}{\sqrt n}+R_2$ ( ozaj formalita)

A limita je potom ozaj hracka.

kontrola:

Autor skryl část textu. Zobrazit/skrýt!

myrek · 13. 03. 2012 01:49

$\lim_{n \to \infty}\frac{1}{\sqrt n}+ln(\sqrt{1+\frac 1n}-\frac{1}{\sqrt n})=$
$=\lim_{n \to 0+} \sqrt n + ln((1+n)^{\frac 1 2}-\sqrt n)$
takze $(1+n)^{\frac 1 2}$ prvni dva cleny $1 + \frac n 2$
prvni dva cleny $ln(1+\frac n 2 - \sqrt n)=\frac n 2 - \sqrt n - \frac{(\frac n 2 -\sqrt n)^2}{2}= \frac {-n^2}{8} + \frac {n} {2} - \sqrt n - \frac n 2 + \frac{n\sqrt n}{2}=\frac {-n^2}{8}-\sqrt n + \frac{n\sqrt n}{2}$
odmocniny z n se vyrusi
tedy vysledek $\frac{-n^2+4n\sqrt n}{8}$
pozn vynechavam ocka a lim

vanok · 13. 03. 2012 13:19 — Editoval vanok (13. 03. 2012 13:50)

↑ myrek:
analysujem tvoju pracu: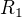 $R_1$
pises
takze $(1+n)^{\frac 1 2}$ prvni dva cleny $1 + \frac n 2$
to je OK az na to ze zlomok mal by byt
$\frac 1 {2n}$

$R_2$
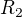
Tu si pouzil upravu ( na danom vyraze) co nie je presna:
pises:
$ln(1+\frac n 2 - \sqrt n)=\frac n 2 - \sqrt n - \frac{(\frac n 2 -\sqrt n)^2}{2}= \frac {-n^2}{8} + \frac {n} {2} - \sqrt n - \frac n 2 + \frac{n\sqrt n}{2}=\frac {-n^2}{8}-\sqrt n + \frac{n\sqrt n}{2}$
treba pracovat stale na vyraze
$\frac{1}{\sqrt n}+ln(\sqrt{1+\frac 1n}-\frac{1}{\sqrt n})=$

A ak\o som pisal treba hladat v tejto etape rozvoj pre
$\ln(1 + \frac n 2-\frac{1}{\sqrt n})$
a ten ma prve dva cleny
$-\frac{1}{\sqrt n}+\frac 16$\frac 1n $^{\frac 32}$

a $R_3$ uz dokazes najst

Edit: kolega ma upozornil, ze presiel z $+\infty$ do $0$
Ale je opatrne napisat, ked sa takato zmena urobi... a akoze ide o rozvoje v novom bode je tiez ziaduce napisat napr toto
V okoli bodu 0, mame nasledujuce rozvoje....

myrek · 13. 03. 2012 13:34

↑ vanok:
nojo jenze ja sem n posunul do nuly takze pracuji na vyrazu
$\sqrt n + ln((1+n)^{\frac 1 2}-\sqrt n)$

vanok · 13. 03. 2012 13:46 — Editoval vanok (13. 03. 2012 13:51)

↑ myrek:,
Prepac, to som si nevsimol ( i ked ide o viazanu premennu, je opatrnejsie alebo zmenit potom pismeno premennej napr m miesto n... ale aspon to napisat... lebo moze sa stat ze aj na skuske si korektor take nevsimne (kazdy je len clovek)).
Ale tak ci tak tie koeficienty musia byt v oboch pripadoch identicke ( pred asociovanymy clenmy)

Dobre pokracovanie

myrek · 13. 03. 2012 16:20 — Editoval myrek (13. 03. 2012 16:25)

↑ vanok:
dobre v pohode
a toto teda neni dobre?

$ln(1+\frac n 2 - \sqrt n)=\frac n 2 - \sqrt n - \frac{(\frac n 2 -\sqrt n)^2}{2}+o(({\frac n 2 - \sqrt n})^2)= \frac n 2 - \sqrt n - \frac{\frac{n^2}{4}-n\sqrt n+n}{2}+o(({\frac n 2 - \sqrt n})^2)=$
$=\frac {-n^2}{8}-\sqrt n + \frac{n\sqrt n}{2}+o(({\frac n 2 - \sqrt n})^2)$

nebot $ln(1+x)=x-\frac {x^2}{2}+...$

vanok · 13. 03. 2012 17:23 — Editoval vanok (13. 03. 2012 17:24)

Ahoj, skutocne su tam chyby
dva platne cleny ( z najnizimy mocninamy ) neznamena, ze netreba pocitat aj trochu vadci rozvoj :Konkretne to znamena, ze treba najsti "STOPY" vsetkych clenov ktore obsahuju danu mocninu co nas zaujima
Tu mame $(\frac n2 -\sqrt n)^3/3$ ktory obsahuje jeden clen co nas zaujima $n\sqrt n)/3$
Pouzi na to tzv "aritmetiku rozvojov"
A potom ten rozvoj nie je $o(n^2)$ ( staci ze to spatne napises a mas zarucenu vylucnu znamku na skuske)

Tak oprav tie chyby.

Inac, som ti dal jednu kompletnu metodu riesenia, tak dufam ze to vsetko nepomiesas.

Dobre pokracovanie a uspech na skuskach

myrek · 15. 03. 2012 23:59

↑ vanok:
okay no nejvic mi dela problem jak poznat jak dlouhy udelat rozvoj
kdyz je ve jmenovateli mocnina n tak to jeste jde ze vim ze bych to mel rozvinout tak abych s tim clenem mohl kratit

Matematické Fórum

#1 13. 03. 2012 00:10

taylor

#2 13. 03. 2012 00:31 — Editoval jardofpr (13. 03. 2012 00:33)

Re: taylor

#3 13. 03. 2012 00:41

Re: taylor

#4 13. 03. 2012 00:44 — Editoval jardofpr (13. 03. 2012 00:47)

Re: taylor

#5 13. 03. 2012 00:59 — Editoval vanok (13. 03. 2012 01:04)

Re: taylor

#6 13. 03. 2012 01:49

Re: taylor

#7 13. 03. 2012 13:19 — Editoval vanok (13. 03. 2012 13:50)

Re: taylor

#8 13. 03. 2012 13:34

Re: taylor

#9 13. 03. 2012 13:46 — Editoval vanok (13. 03. 2012 13:51)

Re: taylor

#10 13. 03. 2012 16:20 — Editoval myrek (13. 03. 2012 16:25)

Re: taylor

#11 13. 03. 2012 17:23 — Editoval vanok (13. 03. 2012 17:24)

Re: taylor

#12 15. 03. 2012 23:59

Re: taylor

Zápatí