Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » metóda prostej iterácie (TOTO TÉMA JE VYŘEŠENÉ)
#1 17. 03. 2012 19:42
metóda prostej iterácie
Ahojte,
trápim sa s metódou prostej iterácie. Mám niekoľko (viac-menej) vzorových príkladov, ale ani ku jednému sa neviem postaviť z toho správneho uhla. Napríklad funkcia f: 
Najskôr graficky separujem korene pre jednotlivé zložky pôvodnej funkcie na 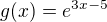 a
a 
kde korene sú 2 a to  a
a  Vhodnosť intervalov si overím pomocou znamienok, kde funkčné hodnoty f(x) na začiatku a na konci intervalu musia mať opačné znamienka.
Vhodnosť intervalov si overím pomocou znamienok, kde funkčné hodnoty f(x) na začiatku a na konci intervalu musia mať opačné znamienka.
Potom prepíšem f(x)=0 do tvaru x=F(x) takže  Urobím deriváciu
Urobím deriváciu 
Teraz by som mal nejako skombinovať deriváciu s každým intervalom aby som videl, či platí Banachova veta.
ak by platilo  malo by to znamenať, že na danom intervale je funkcia kontrahovateľná a že môžem iterovať.
malo by to znamenať, že na danom intervale je funkcia kontrahovateľná a že môžem iterovať.
Tomu ako vyčísliť hodnotu F'(x) pre každé x z daného intervalu však celkom nerozumiem. Môžem tam dosadiť krajné body intervalov a z nich vypočítať hodnoty ? Čo mi zaručuje, že keď podmienka platí pre krajné body, tak platí aj pre každé x patriace do daného intervalu ?
Ďakujem za pomoc a nakopnutie správnym smerom
Offline
- (téma jako vyřešené označil(a) etchie)
#2 17. 03. 2012 23:04
Re: metóda prostej iterácie
metódu prostej iterácie si už viem prepísať do algoritmu, konkrétne pre Matlab
Z tohoto pohľadu teda rozumiem tejto metóde až na tú časť, ktorú som popisoval vyššie
skúsim to z opačného konca:
odhad chyby pri tejto metóde sa počíta ako 
kde  je skutočný koreň a
je skutočný koreň a 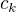 je koreň vypočítaný v poslednej iterácii
je koreň vypočítaný v poslednej iterácii
zároveň musí platiť  kde
kde  pre
pre 
práve toto  si neviem zdôvodniť a ani neviem ako ho mám zakomponovať do výpočtu.
si neviem zdôvodniť a ani neviem ako ho mám zakomponovať do výpočtu.
keď si ho zvolím napr. ako hodnotu ľavej strany intervalu, tak môj algoritmus počíta rovnako dobre ako WolframAlpha, ale nerozumiem tomu :-(
Offline
#3 17. 03. 2012 23:48
Re: metóda prostej iterácie
ešte jedno upresnenie čomu to vlastne nerozumiem je koeficient kontraktívnosti
je koeficient kontraktívnosti
a vo všetkých vzorových príkladoch sa náhle objaví 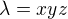 a len sa konštatuje, že
a len sa konštatuje, že 
ale odkiaľ sa berie konkrétna hodnota  ?
?
mám v tom stále dosť chaos
Offline
#5 18. 03. 2012 10:36
Re: metóda prostej iterácie

vie mi niekto vysvetliť odkiaľ sa nabrala tá 1/3 ?
supremum to nie je podľa mňa, ale netuším odkiaľ sa to berie,
v predošlom príklade by to aj sedelo, že ide o supremum, ale tu nie
nakoniec sa zrejme "doiterujem" k pochopeniu prostej iterácie, ale ostáva ešte aj tento nejasný bod
ďakujem
Offline
#6 18. 03. 2012 12:32 — Editoval vanok (18. 03. 2012 12:33)
Re: metóda prostej iterácie
Ahoj ↑ etchie:, je majoracia derivacie
je majoracia derivacie  v danom intervale.
v danom intervale.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 18. 03. 2012 18:34
Re: metóda prostej iterácie
↑ etchie:
pozri sem
http://en.wikipedia.org/wiki/Contraction_mapping
Co mas vo skriptach?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 18. 03. 2012 19:05
Re: metóda prostej iterácie
↑ vanok:
učím sa z týchto skrípt (strany 12 až 14)
Skriptá numerické metódy
potom ešte aj z vlastných poznámok z prednášky, ale tam číselná hodnota lambda tiež vystupuje spôsobom "deus ex machina"
Offline
#10 20. 03. 2012 09:48
Re: metóda prostej iterácie
↑ etchie:,
Preletel som tvoj material.
Moju poznamku ↑ vanok:, treba dat do suvisu z vetou 1.4 ( str 12)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 20. 03. 2012 19:06
Re: metóda prostej iterácie
tu je môj postup pri výpočte príkladu 1.5![kopírovat do textarea $\varphi'(x)=\frac{1}{3\sqrt[3]{(x+1)^2}}$](/mathtex/6e/6ebb88d964b60eb9249dc47f15f2e167.gif)
 pre
pre 
počítačová funkcia pre určenie suprema asi veľmi nebude k dispozícii, preto bude stačiť maximum, takže to čo skutočne vypočítam je teda
teda 
maximum počítam iba z krajných hodnôt intervalu teda musím predpokladať, že  na intervale
na intervale  má vhodný priebeh a maximum je naozaj v jednom z krajných bodov (ak by to neplatilo, tak vôbec neviem čo s tým).
má vhodný priebeh a maximum je naozaj v jednom z krajných bodov (ak by to neplatilo, tak vôbec neviem čo s tým).
ďalej zistím, že  a preto
a preto  podľa postupu zo strany 12
podľa postupu zo strany 12
koeficient  budem používať pre odhad chyby, aby som vedel skončiť pri dosiahnutí požadovanej presnosti
budem používať pre odhad chyby, aby som vedel skončiť pri dosiahnutí požadovanej presnosti
zároveň postup v príklade 1.5 hovorí, že: platí
platí 
s čím ja nesuhlasím lebo 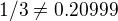
resp. ani nerozumiem načo tam tá  vôbec je uvedená ani odkiaľ sa tam vzala
vôbec je uvedená ani odkiaľ sa tam vzala
Offline
#12 20. 03. 2012 19:23 — Editoval etchie (20. 03. 2012 19:42)
Re: metóda prostej iterácie
↑ etchie:
hm, teraz keď pozerám na svoj práve poslaný príspevok tak sa mi zdá, že tá  pochádza vlastne z
pochádza vlastne z  kde vzorec začína zlomkom
kde vzorec začína zlomkom  a premenné sú iba v menovateli, čo znamená, že nech je x akékoľvek tak výsledok je limitovaný zhora
a premenné sú iba v menovateli, čo znamená, že nech je x akékoľvek tak výsledok je limitovaný zhora 
Edit: no neplatí to pre všetky x, keď sa x blíži k -1 tak hodnoty idú nad 1/3, takže nič z toho
stále mi to však nevysvetľuje, či si mám zvoliť  alebo
alebo  alebo to je jedno ?
alebo to je jedno ?
Offline
#13 22. 03. 2012 00:13
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: metóda prostej iterácie
Zdravím,
celé téma jsem úplně podrobně nepročítala (mám opět pocit, že se odvážně pouštíš do samostudia? :-) je tak?).
Ano,  je "limitována" hodnotou 1/3 na intervalu od 1 do 2 (Tvá poznámka pro x=-1 na tomto intervalu nemá význam). Zvolíme takové
je "limitována" hodnotou 1/3 na intervalu od 1 do 2 (Tvá poznámka pro x=-1 na tomto intervalu nemá význam). Zvolíme takové  , které umíme počítat (ohodnotit) bez použití techniky. Pokud bychom chtěli
, které umíme počítat (ohodnotit) bez použití techniky. Pokud bychom chtěli  zpřísňovat, tak bychom museli použit pomocnou metodu na odmocnění (což se nám nebude chtít).
zpřísňovat, tak bychom museli použit pomocnou metodu na odmocnění (což se nám nebude chtít).
To proto, že numerické metody primárně pomáhají přibližně vyřešit to, co nemůžeme vyřešit přesně a nepoužíváme techniku (např. na pustém ostrově :-)
Offline
#14 22. 03. 2012 22:03
Re: metóda prostej iterácie
↑ jelena:
no teraz to je tiež samoštúdium, ale už povinné. niektoré veci neboli na prednáške preberané. alebo mne neboli zrejmé.
hľadal som aj v iných zdrojoch + po rozobratí problému tu na fóre, mi z toho vychádza, že hodnota  nebude až tak kritická pri tejto metóde. teda že hodnota
nebude až tak kritická pri tejto metóde. teda že hodnota  je zrejme rovnako dobrá ako
je zrejme rovnako dobrá ako  , hlavne že sú obe
, hlavne že sú obe  a teda dochádza ku kontrakcii a iteráciami sa výpočet približuje k pevnému bodu. nejak takto to zatiaľ chápem, tak dúfam, že nie som už ďaleko.
a teda dochádza ku kontrakcii a iteráciami sa výpočet približuje k pevnému bodu. nejak takto to zatiaľ chápem, tak dúfam, že nie som už ďaleko.
zrejme sa musím zamerať na vzťah  , ktorý som zatiaľ ešte nepochopil, ale vyzerá že ten je kľúčom k chápaniu toho celého
, ktorý som zatiaľ ešte nepochopil, ale vyzerá že ten je kľúčom k chápaniu toho celého
dôležité je len to, aby  a vtedy
a vtedy 
Offline
#15 22. 03. 2012 22:23
Re: metóda prostej iterácie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 24. 03. 2012 09:45
Re: metóda prostej iterácie
↑ vanok:
no veď práve tá stránka 11...
vysypaný sáčok s písmenkovou polievkou, aj Popoluška to zrejme mala ľahšie
odhliadnuc od polievky, tá stánka produkuje pre mňa viac otázok, než som mal doteraz
- čo je to úplný metrický priestor
- čo je to cauchyovská postupnosť
- trojuholníková nerovnosť
ale budem skúšať ďalej sa cez to nejako prelúskať
mimochodom, pýtal som sa spolužiakov ako rozumejú metóde prostej iterácie, tak vačšina bola ticho a jeden povedal, že veď to je úplne ľahké, iba treba pochopiť Banachovu vetu. Hneď som sa teda opýtal ako sa vypočíta lambda, no a odpoveďou bolo zas ticho. :-)
Offline
#17 24. 03. 2012 09:54 — Editoval vanok (24. 03. 2012 09:58)
Re: metóda prostej iterácie
↑ etchie:,
aha, to tie "zakladne pojmy " si este neasimiloval.
Co je velmi pozitivne, si urcil, veci co ti treba v priorite nastudovat.
Tvoja metoda, je ucinna ak doplnis vsetko co ti teraz robi problemy.
Na tie tri pojmy, co si vyssie napisal, mozes pouzit aj wikipediu
Napriklad
http://cs.wikipedia.org/wiki/Troj%C3%BA … _nerovnost
http://en.wikipedia.org/wiki/Triangle_inequality
EN verzia je casto podrobnejsia ako CZ alebo SK.
Otazka okolo  , na to, Banachovej vete, je ozaj presne treba, vsetko co si napisal vyssie... a pridal by som este aj sucet geometrickej rady ( ale to iste vies)
, na to, Banachovej vete, je ozaj presne treba, vsetko co si napisal vyssie... a pridal by som este aj sucet geometrickej rady ( ale to iste vies)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 20. 04. 2012 16:14
Re: metóda prostej iterácie
ja len toľko, že zápočet z matematiky bol úspešný a podľa všetkého to bol najlepší výsledok v skupine.
za čo ďakujem všekým Vám, ktorí ste mi ochotne a vytrvalo odpovedali na moje otázky. a to nielen v tomto vlákne ale aj v iných, kde som niečomu nerozumel.
ešte to síce nie je skúška, ale je to prvý nevyhnutný krok k nej a ten ma vééééľmi teší. :-)
ďakujem veľmi pekne za všetky rady, ochotu a výdrž.
Offline
#20 11. 11. 2012 15:41
Re: metóda prostej iterácie
ja sa tiez odvolavam na tuto knizku, zameram sa na uz preberany priklad 1.5 (metoda prostej iteracie):
z tohto tu si vypocitam x... pocital som to bud tak, ze som si vsetko okrem  dal na pravu stranu a z toho mi vyslo:
dal na pravu stranu a z toho mi vyslo:

alebo som este skusal dat vsetko okrem 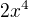 n pravu stranu a vyslo mi z toho:
n pravu stranu a vyslo mi z toho:
x=![kopírovat do textarea $\sqrt[4]{0,25-2,5x^{2}-3x^{3}}$](/mathtex/5a/5ac60e241812ec8ec005c8767a31e93d.gif)
aproximacia korena ma vyjst 0,2716, cize interval zvolim napr. <0,2;0,3>, ale tu nastava problem..
pri nultom kroky, i=0 -> 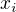 =0,2 mi pri prvom kroku i=1, x bude rovnat 0,299599733 resp. 0,5835989439.
=0,2 mi pri prvom kroku i=1, x bude rovnat 0,299599733 resp. 0,5835989439.
kde je problem, v com je problem??
ked som sa profesora pytal na  tak mi povedal, ze si mam len dosadit tych 0,2.. cize tu podmienku mam akoby ignorovat...
tak mi povedal, ze si mam len dosadit tych 0,2.. cize tu podmienku mam akoby ignorovat...
ĎAKUJEM
Offline
#21 11. 11. 2012 22:14
Re: metóda prostej iterácie
↑ meno112:
no neviem kde tam je chyba, lebo keď si nahodím ten tvoj vzorec "x = druhá odmocnina ...",
a začnem s x = 0,2 tak potom prvá iterácia je ako píšeš 0,299...
potom vezmem výsledok 0,299... ako nové x a tak dokola, až to pekne konverguje k požadovanému výsledku 0,2716
cca 11-ta iterácia vracia požadovaný výsledok.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » metóda prostej iterácie (TOTO TÉMA JE VYŘEŠENÉ)

 na intervale
na intervale 
 , ktorú som náhodou trafil a preto aj výpočet pomocou algoritmu bol ok
, ktorú som náhodou trafil a preto aj výpočet pomocou algoritmu bol ok