Matematické Fórum

Andrejka3

Dobrý den.
Napadla mě myšlenka:
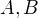Buď $\textbf{G}=(G,*,',e)$ grupa. $A,B$ její podgrupy.
Musí být nutně $M:=AB \cap BA$ podgrupa?
Definuji $AB=\{a*b;\;a \in A \;\wedge\;b \in B\}$ .
Jistě je $e \in M$ ,
$c \in M \Rightarrow c' \in M$ .
Uzavřenost množiny M na binární grupovou operaci neumím dokázat. Myslím si, že obecně se nejedná o podgrupu, ale nemám protipříklad.

Při hledání protipříkladu lze využít tvrzení:
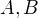Buď $\textbf{G}=(G,*,',e)$ grupa. $A,B$ její podgrupy.
$AB$ je podgrupou $G$ , právě když $AB=BA$ .

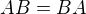Našel by někdo protipříklad proti mé domněnce? Nebo důkaz?

Pavel Brožek · 26. 03. 2012 19:04

Pozorování: Pokud bude alespoň jedna z grup A a B normální podgrupa, pak je M podgrupa.

Důkaz (už pouze uzavřenosti na binární grupovou operaci):

Mějme dva prvky $g,\tilde g\in M$ . Pak můžeme psát $g=a_1b_1=b_2a_2$ a $\tilde g=\tilde a_1\tilde b_1=\tilde b_2\tilde a_2$ pro nějaké $a_1, a_2, \tilde a_1, \tilde a_2\in A$ a $b_1, b_2, \tilde b_1, \tilde b_2\in B$ .

Pro součin těchto prvků platí

(1) $g\tilde g=a_1b_1\tilde a_1\tilde b_1=b_2a_2\tilde b_2\tilde a_2.$

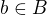BÚNO předpokládejme, že B je normální podgrupa. Pak platí $\tilde a_1^{-1}b_1\tilde a_1=b$ pro nějaké $b\in B$ . Tuto poslední rovnost přenásobíme $\tilde a_1$ zleva a dostaneme $b_1\tilde a_1=\tilde a_1 b$ . Dosadíme do první části (1).

(2) $g\tilde g=a_1\tilde a_1 b\tilde b_1.$

Vidíme tedy, že $g\tilde g\in AB$ . Analogicky bychom díky normálnosti podgrupy B „prohodili“ prvky $a_2\tilde b_2$ a dostali bychom, že $g\tilde g\in BA$ a celkově $g\tilde g\in M$ .

Jestliže chceme najít protipříklad, musíme hledat podgrupy A a B takové, že obě nejsou normální.

Andrejka3 · 26. 03. 2012 19:08

↑ Pavel Brožek:
Děkuji!

Pavel Brožek

Podobně ani jedna z těch grup v protipříkladu nemůže být kvazinormální (kvazinormální podgrupa komutuje s každou podgrupou, každá normální grupa je kvazinormální). Musíme najít dvě podgrupy A, B takové, aby $AB\neq BA$ .

Andrejka3

↑ Pavel Brožek:
Ano, to každopádně. Je to vidět z tvrzení v mém prvním příspěvku:
Kdyby 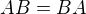$AB=BA$ , je $M=AB$ a podle onoho tvrzení pak je $M$ podgrupou.
Bylo mi hned jasné, že komutativní grupy toto splní automaticky.
Normální grupy jsem neověřila, proto jsem ráda za ten důkaz.
No a kvazinormální grupy jsem prakticky neznala :)
edit: komutativní místo komutující.

Pavel Brožek

↑ Andrejka3:

Já jsem kvazinormální podgrupy také neznal. Já se v tom snažím zorientovat, takže si to postupně ujasňuji. Ten můj důkaz byl vlastně zbytečně složitý, protože normálnost podgrupy implikuje, že ta podgrupa komutuje s celou grupou, tedy speciálně i s její libovolnou jinou podgrupou. A s využitím toho tvého tvrzení máme okamžitě, že žádná z těch podgrup v protipříkladu nemůže být normální.

Takže můj cíl je najít teď nějakou grupu s dvěma nekomutujícíma podgrupama. I kdyby nevyvracela tu tvou doměnku, tak by nám mohla pomoct uvědomit si nové věci :-).

Pozn.: V angličtině se komutující podgrupy nazývají „permuting subgroups“. Nepovedlo se mi ale žádné nikde najít.

Pavel Brožek · 26. 03. 2012 20:40

Jestli jsem neudělal chybu, tak protipříkladem je dihedrální grupa a její podgrupy

$A=\{R_0,S_0\}\nl B=\{R_0,S_1\}$

Mělo by být

$AB=\{R_0, S_0, S_1,R_2\}\nl BA=\{R_0, S_0, S_1,R_1\}\nl AB\cap BA=\{R_0, S_0, S_1\}$

a to není grupa, protože $S_0S_1=R_2\not\in AB\cap BA$ .

Pavel Brožek

Ještě dodatek:

já napsal(a):
Takže můj cíl je najít teď nějakou grupu s dvěma nekomutujícíma podgrupama. I kdyby nevyvracela tu tvou doměnku, tak by nám mohla pomoct uvědomit si nové věci :-).

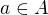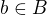Jakmile $AB\neq BA$ , tak máme protipříklad, protože BÚNO existuje $g\in AB$ takové, že $g\not\in BA$ . Platí tedy $g=ab$ pro nějaká $a\in A$ a $b\in B$ . Protože jednotkový prvek je v A i B, tak prvky a a b jsou prvky AB i BA a tedy i M. Kdyby M byla grupa, pak i součin ab je z M a tedy je $g=ab\in BA$ , což je spor.

Andrejka3 · 26. 03. 2012 22:00

↑ Pavel Brožek:
Díky moc!
Dneska jsem vyřešila jeden příklad na grupy a tohle mi začalo vrtat hlavou a nemohla jsem na to přijít.
Všechno si projdu, jestli tomu rozumím a kdyžtak se ještě zeptám. Díky.
A.

Andrejka3 · 27. 03. 2012 10:40

↑ Pavel Brožek:
Ano, všechno je v pořádku.
V tom ↑ odkazu: na kvazinormální podgrupy jsou též odkazy na PDF o nich. Takže beztak nějaká zajímavá teorie. Spoustu lákadel v té matematice :)

Matematické Fórum

#1 26. 03. 2012 18:18 — Editoval Andrejka3 (26. 03. 2012 18:19)

AB \cap BA neni podgrupa?

#2 26. 03. 2012 19:04

Re: AB \cap BA neni podgrupa?

#3 26. 03. 2012 19:08

Re: AB \cap BA neni podgrupa?

#4 26. 03. 2012 19:34 — Editoval Pavel Brožek (26. 03. 2012 19:35)

Re: AB \cap BA neni podgrupa?

#5 26. 03. 2012 19:59 — Editoval Andrejka3 (26. 03. 2012 20:09)

Re: AB \cap BA neni podgrupa?

#6 26. 03. 2012 20:10 — Editoval Pavel Brožek (26. 03. 2012 20:14)

Re: AB \cap BA neni podgrupa?

#7 26. 03. 2012 20:40

Re: AB \cap BA neni podgrupa?

#8 26. 03. 2012 21:25 — Editoval Pavel Brožek (26. 03. 2012 21:25)

Re: AB \cap BA neni podgrupa?

já napsal(a):

#9 26. 03. 2012 22:00

Re: AB \cap BA neni podgrupa?

#10 27. 03. 2012 10:40

Re: AB \cap BA neni podgrupa?

Zápatí