Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 31. 03. 2012 22:17
Re: Zoradenie fci casovych zlozitosti
10000x opakovaní příslušného výpočtu trvalo v sekundách:
a - 0.54
b - 2.54
c - 1.64
d - 0.70
e - 0.76
f - 0.37
g - 0.65
h - 1.03
Zajímavá je možnost b) která vyšla nejpomalejší, což jsem vůbec nepředpokládal
Offline
#3 31. 03. 2012 22:25 — Editoval pizet (31. 03. 2012 22:40)
Re: Zoradenie fci casovych zlozitosti
↑ mák:
Ahoj.
Celkom mi nie je jasné, že čo si ty počítal.
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#4 31. 03. 2012 22:31 — Editoval pizet (31. 03. 2012 22:39)
Re: Zoradenie fci casovych zlozitosti
↑ milwoukee:
Ahoj.
milwoukee napsal(a):
Staci ked si podosadzam za n napriklad od 1 do 5 a porovnam?
To určite nestačí. Nejaká funkcia môže mať pre malé n menšie hodnoty ako druhá ale pre n idúce do nekonečna môže byť situácia úpne iná.
Príklad. Uvážme funkcie a
a 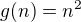 .
.
Je vidieť, že pre malé n vracia funkcia f väčšie hodnoty ako funkcia g. Avšak to už neplatí pre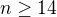 .
.
Teda tu by tvoj postup určite neuspel.
Z kade máš túto úlohu? Máš k tomu aj nejaké teoretické znalosti? Je ti napríklad známa notácia "veľké Ó"?
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#5 31. 03. 2012 22:39 — Editoval milwoukee (31. 03. 2012 22:41)
Re: Zoradenie fci casovych zlozitosti
↑ pizet:
Ahoj mam viac menej nejake teoreticke znalosti. Ak myslis omikron tak f patri O(g) znamena ze f rastie nanajvys tak rychlo ako g.
To s tym dosadzanim som si aj myslel ze nepojde tak , ale potom ma nenapada ako riesit tento typ prikladov...
Jedine zeby delenim limit tych rychlosti, ale neda sa to aj nejak rychlejsie?
Offline
#6 31. 03. 2012 22:42 — Editoval pizet (31. 03. 2012 22:42)
Re: Zoradenie fci casovych zlozitosti
↑ milwoukee:
No môžeš si napríklad typnúť, že ktorá funkcia bude pre veľké n nadobúdať väčšie hodnoty a potom sa to pokúsiť formálne dokázať.
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#8 31. 03. 2012 22:46 Příspěvek uživatele pizet byl skryt uživatelem pizet. Důvod: Hlúposť
#10 31. 03. 2012 22:53
Re: Zoradenie fci casovych zlozitosti
Napríklad môžeš porovnať rýchlosť rastu funkcií a
a 
tak, že uvážiš, že ,
,
teda 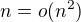 .
.
Záver je, že funkcia  rastie postatne pomalšie než funkcia
rastie postatne pomalšie než funkcia  .
.
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#11 31. 03. 2012 23:02
Re: Zoradenie fci casovych zlozitosti
Obecne se to resi vetsinou tak, ze se funkce prevedou do exponencialni funkce tvaru 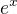 a pak se porovnavaji ty ruzne fce x, pujde to jednoduseji, vetsinou to bude jen nejaka konstanta krat linearni/kvadraticka fce...
a pak se porovnavaji ty ruzne fce x, pujde to jednoduseji, vetsinou to bude jen nejaka konstanta krat linearni/kvadraticka fce...
Pro faktorial bude potreba prvne pouzit nejaky rozumny odhad (treba Stirlinguv vzorec)...
Jinak na prvni pohled bych rekl, ze nejrychleji rostouci bude d) a nejpomaleji c)...
Offline
#13 01. 04. 2012 01:22 — Editoval pizet (01. 04. 2012 01:26)
Re: Zoradenie fci casovych zlozitosti
↑ milwoukee:
Použíl som definíciu všeobecnej mocniny :
Nech  a
a 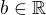 , potom definujeme
, potom definujeme 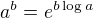 .
.
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
#15 01. 04. 2012 16:15
Re: Zoradenie fci casovych zlozitosti
milwoukee napsal(a):
Dik , este by som sa rad spytal ako napr.
pretavim na ten tvar
, je nejaky vzorec na to?
Aha to podla toho isteho vzorca v zmysle??
Správne, i keď tie logaritmy, ktoré som písal v tej definícii sú prirodzené.
milwoukee napsal(a):
A mozme pri logaritmoch zanedbavat zaklady v takychto pripadoch?
No môžeme. Je známa nasledujúca definícia:
Ak sú  , tak definujeme
, tak definujeme 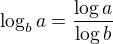 .
.
Z toho plynie, že logaritnus o ľubovoľnom základe je len konštanta krát logaritmu o základe e a konštanty pri určovaní asymptotickej časovej zložitosti zanedbávame. Väčšinou sa píše proste 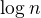 .
.
Pozor! Napríklad pri funkcii 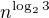 naopak veľmi záleží na tom, aký má logaritmus v exponente základ.
naopak veľmi záleží na tom, aký má logaritmus v exponente základ.
Do you follow my way? Or you just see a black stain swimming in the Milky Way ...
KSP je určený pre študentov základných a stredných škôl, ktorí majú záujem naučiť sa niečo z oblasti algoritmov, logických úloh, programovania a informatiky.
Offline
 ∗
∗

 plati, ze
plati, ze  ale neviem ako pri tych zlozitejsich...
ale neviem ako pri tych zlozitejsich...