Matematické Fórum

lajk · 31. 03. 2012 14:49

ahoj
potřeboval bych nakopnout, jak začít s řešením, stačí 1-2 příklady, díky.

vanok · 31. 03. 2012 15:00

Ahoj ↑ lajk:,
Metoda je vzdy podobna.
Vyjadri, vzdy jednu bazu tvojho priestoru... a napis v tejto bazy, tvoje "vektory"... vo forme suradnic.
Napriklad. Baza priestoru $P_2(x)$ je $(1,x, x^2)$
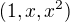
Tvoje vektory sa pisu takto $(1;1,0);1;-1;0);(2;1;-1)$

Staci?

lajk · 31. 03. 2012 22:22

mám problém
6)c)
vyjde mi
1 1 0 0
0 1 1 0
0 0 1 1
0 0 0 1
To je triviální řešení tím pádem LN, ale ve výsledcích je LZ. Tak jak to je?

a jak na tu sedmičku?
díky.

vanok · 31. 03. 2012 23:21

↑ lajk:
vektory v 6c) sa pisu
$(0;1; 0;0); (0;1;1;0); (0;0; 1;1); (1;0;0;1)$
Suradnice maju vzdy dany poriadok podla vektorov baze ( a tam bol maly chytak, ze zmenili narocky poriadok)... a skutocne lahko ukazes ze ide o LN vektory ( chyba v zadani vysledku v knihe)

V 7) pouzi definiciu LN
x,y,z LN
znamena, ze ax+by+cz=0 ma len trivialne riesenie a=b=c=0 (*)

A teraz predpokladaj
ze mas A(x+y)+B(y+z)+C(z+x)=0 a urav tvoju rovnost na formu aby si mohol pouzit (*) a dokonci vdaka jednoduchemu systemu (3,3)

lajk · 01. 04. 2012 16:28

Můžeš prosím víc k té sedmičce?
A(x+y)+B(y+z)+C(z+x)=0
tuto rovnici mám roznásobit? Nevím jak dál.

vanok · 01. 04. 2012 17:23

↑ lajk:
to da $(A+C)x+(A+B)y+ (B+C)z=0$
co da vdaka predpokladu o x; y, z ze

$A + C=0$
$A+ B =0$
$B + C=0$

Vyries tento system a ak A=B= C=0 je jeho jedinne riesenie , tak mas LN.... ( ak nie....)

A zvysok sa robi tak isto.

lajk · 01. 04. 2012 17:52

Super už jsem to skoro vše spočítal a sedí to díky moc.

vanok · 01. 04. 2012 18:43

↑ lajk:,
Tak pocitam na teba, ze budes tu na tuto temu inym radit.
Dobre pokracovanie.

Matematické Fórum

#1 31. 03. 2012 14:49

lineární závislost/nezávislost prvků v prostoru

#2 31. 03. 2012 15:00

Re: lineární závislost/nezávislost prvků v prostoru

#3 31. 03. 2012 16:21 Příspěvek uživatele lajk byl skryt uživatelem lajk. Důvod: doublepost

#4 31. 03. 2012 22:22

Re: lineární závislost/nezávislost prvků v prostoru

#5 31. 03. 2012 23:21

Re: lineární závislost/nezávislost prvků v prostoru

#6 01. 04. 2012 16:28

Re: lineární závislost/nezávislost prvků v prostoru

#7 01. 04. 2012 17:23

Re: lineární závislost/nezávislost prvků v prostoru

#8 01. 04. 2012 17:52

Re: lineární závislost/nezávislost prvků v prostoru

#9 01. 04. 2012 18:43

Re: lineární závislost/nezávislost prvků v prostoru

Zápatí