Matematické Fórum

Pavel Brožek

Zdravím,

mám funkci reálné proměnné x

$f(x)=\int_0^{\infty}\frac{t^2}{t^2+x^2}g(t)\,\d t,$

kde $g$ je taková funkce, že integrál konverguje pro všechna $x\in\mathbb{R}$ .

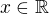Pomocí residuové věty se snadno zjistí, že pro hezkou $g$ holomorfní na celém $\mathbb{C}$ se funkce f chová pro $x\to\infty$ jako $\frac1x$ .

Je vidět, že $\lim_{x\to\infty}x f(x)$ je konečné nenulové číslo i nějak jednodušeji a s mnohem menšími nároky na funkci $g$ ?

Jen mě to tak zajímá, vlastně to na nic nepotřebuju vědět :-).

vanok · 04. 04. 2012 14:16

Ahoj ↑ Pavel Brožek:,
Aj ja vidim, ze pre $g(x)= \frac 1 {x^{1+\varepsilon }}$ kde $\varepsilon >0$ da konvergujuci integral.
Ale na co to sluzi? Priklad, funcie definovanou pomoocu integralu?

Pavel Brožek · 04. 04. 2012 14:34

↑ vanok:

Ahoj,

tenhle integrál vznikne pokud máme v kvantovce sféricky symetrický separabilní potenciál $V=-\lambda|g\rangle\langle g|$ kde stav g je zadán v impulsové reprezentaci $\langle p|g\rangle=g(p)$ . Když pak hledáme vztah mezi parametrem $\lambda$ a energií vázaného stavu popsanou pomocí proměnné $\kappa$ (pro energii platí $E=(\mathrm{i}\kappa)^2=-\kappa^2$ ), dostaneme vztah

$\lambda^{-1}=\int_0^{\infty}\frac{p^2}{p^2+\kappa^2}|g(p)|^2\,\d p.$

Pro některé potenciály (např. $g(p)=\frac{1}{\sqrt{p^2+\alpha^2}}$ nebo $g(p)=\frac{1}{p^2+\alpha^2}$ , $\alpha>0$ ) vychází vztah mezi $\lambda$ a $\kappa$ opravdu hezky. Když se na to ale teď dívám, tak pro ten druhý potenciál ten pokles v nekonečnu nevychází s první mocninou, ale s druhou. Tak to asi nebude tak jednoduché.