Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 04. 2012 16:22
- (-anicka-)

- Zelenáč
- Příspěvky: 12
- Reputace: 0
Aritmetická postupnosť
Zdravím, prosím o pomoc s týmto príkladom. Vopred ďakujem :)
Ak v AP je súčet prvých n členov  =n.(an+b), potom člen
=n.(an+b), potom člen 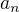 = ...
= ...
Offline
#4 06. 04. 2012 16:37
- (-anicka-)

- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: Aritmetická postupnosť
↑ Siroga:
ale to nie je  ale
ale 
Offline
#5 06. 04. 2012 16:44
Re: Aritmetická postupnosť
Jstlž jst schpn přčst tt, mžt njt dbr zmstnn jk prgrmtr.
Offline
#6 06. 04. 2012 16:49
- (-anicka-)

- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: Aritmetická postupnosť
↑ Siroga:
aha ..:).. dakujem ;)
Offline
#7 06. 04. 2012 16:55
#9 06. 04. 2012 18:41 — Editoval (-anicka-) (06. 04. 2012 18:44)
- (-anicka-)

- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: Aritmetická postupnosť
v knihe je správna odpoveď  :/...hm?
:/...hm?
Offline
#10 06. 04. 2012 19:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Aritmetická postupnosť
↑ (-anicka-):
↑ Siroga:
Zdravím,
když do zápisu  dosadíš
dosadíš 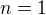 , potom ve skutečnosti máš
, potom ve skutečnosti máš  . A když to dáš dohromady s kolegou↑ Siroga:, tak bys měla mít své vyjádření. V pořádku? Děkuji.
. A když to dáš dohromady s kolegou↑ Siroga:, tak bys měla mít své vyjádření. V pořádku? Děkuji.
Offline
#11 07. 04. 2012 12:18 — Editoval peter_4 (07. 04. 2012 14:58)
Re: Aritmetická postupnosť
![kopírovat do textarea $ S_{n}=n*[a_{1}+a_{n}]/2 $](/mathtex/ac/ac12febe7e2e8daeb8c8548a53e5733d.gif)

![kopírovat do textarea $ S_{n}=n*[a_{1}+a_{1}+(n-1)*d]/2 $](/mathtex/ed/ed2842d80138b20dae0218789dac2c48.gif)
![kopírovat do textarea $ n*[a_{1}+a_{1}+(n-1)*d]/2 = n.(a.n + b) $](/mathtex/af/af5abaeb40d7e10ff423d3717577337e.gif)


Je to sice delší, ale oto horší postup :)
Stejně je to nějaký divný, protože ta diference (dá se zjistit samo i z tohoto tvaru)
an=+a1-a1+2(na+b)-a1
an=a1+2(na+b)-2a1
an=a1+ (n-1) * 2(na+b-a1) /(n-1)
Ta diference sice vyjde nějaké číslo závislé na "a" a "b", což je v pořádku, ale už není v pořádku, aby se diference měnila podle počtu členů v aritmetické posloupnosti "n"
Offline
#12 07. 04. 2012 21:34
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Aritmetická postupnosť
↑ peter_4:
Zdravím,
podle poznámky, kterou jsem napsala v příspěvku ↑ jelena:  , potom
, potom  a diference není závislá na n. Celé odvození jsem neprocházela, podívám se zítra.
a diference není závislá na n. Celé odvození jsem neprocházela, podívám se zítra.
V úvodním tématu ovšem nevidím žádný dotaz na diferenci. Co je tedy účelem příspěvku ↑ peter_4: ? Děkuji.
Offline

 a jestli z toho chceš vyjádřit
a jestli z toho chceš vyjádřit 




