Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » objem rotacneho telesa (TOTO TÉMA JE VYŘEŠENÉ)
#1 10. 04. 2012 16:28 — Editoval Vlad-777 (10. 04. 2012 16:32)
objem rotacneho telesa
zdravim
mam vypocitat objem rotacneho telesa, ktory vznikne rotaciou grafu funkcie y=1/x okolo osi x v intervale
chapem ze zakladom je vypocitat integral tej funkcie, ale akosi mi nejde do hlavy to, ze je to divergentne, ved sa to blizi k nule nie? http://www.wolframalpha.com/input/?i=in … %2C+1..inf
http://www.wolframalpha.com/input/?i=1%2Fx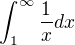
Offline
- (téma jako vyřešené označil(a) jelena)
#2 10. 04. 2012 17:05
Re: objem rotacneho telesa
↑ Vlad-777:
Dobrý den,
ano, jde o nevlastní integrál vlivem horní meze, proto je nutno použít příslušnou metodu řešení.
Offline
#3 10. 04. 2012 17:11 — Editoval jardofpr (10. 04. 2012 17:26)
Re: objem rotacneho telesa
ahoj ↑ Vlad-777:
áno, je pravda, že  , to ale nie je postačujúca podmienka k tomu, aby bol nevlastný integrál konečný ..
, to ale nie je postačujúca podmienka k tomu, aby bol nevlastný integrál konečný ..
táto funkcia "ide k nule" príliš pomaly, preto obsah plochy pod jej grafom nie je ohraničený na danom intervale
dá sa na to pozrieť z pohľadu nekonečného súčtu:
pod grafom funkcie môžme napríklad urobiť obdĺžniky so stranami dĺžky  a
a  pre každé prirodzené
pre každé prirodzené 
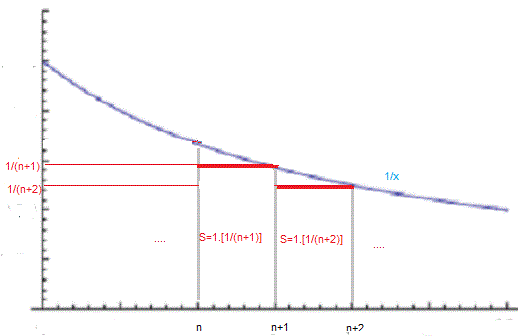
budeme mať 
súčet radu napravo nie je konečné číslo
Offline
#4 10. 04. 2012 17:37
#6 10. 04. 2012 20:47
#8 10. 04. 2012 22:28
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » objem rotacneho telesa (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $\pi \cdot \int_{1}^{\infty }\frac{dx}{x^{2}}=\lim_{c\to\infty }\pi \cdot \int_{1}^{c}x^{-2}dx=\pi \cdot \lim_{c\to\infty }[-\frac{1}{x}]_{1}^{c}$](/mathtex/8a/8adadf69499036d102aeacb4f1358003.gif) atd. :)
atd. :)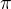 a ne 3,14 :)
a ne 3,14 :)