Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 04. 2012 15:03 — Editoval souteh (11. 04. 2012 19:27)
Vyšetření množiny bodů
Zdravím, potřeboval bych pomoct s pochopením tohoto typu příkladů. Vůbec tomu nerozumím, při hodinách v tom absolutně tápu a zítra z toho mám psát test. Snažil jsem se hledat, zkoušet...nic.
Např.:
1.Vyšetři množinu středů všech kružnic, které se dotýkají kružnice k(S;5cm) a procházejí bodem M. |SM|=3cm
nebo
2.Urči množinu všech bodů X roviny, jejichž poměr vzdáleností od bodu F a přímky q je:
a) 2
b) 1
c) 1/2
q: x-3=0
F[0;1]
3.Je dána přímka p a bod M, |Mp|=6cm. Vyšetři množinu středů všech kružnic, které procházejí bodem M a dotýkají se p.
Prosím o obecný postup tohoto typu příkladů, pokud možno i s řešením těchto tří konkrétních.
Předem moc díky!
Offline
#2 13. 04. 2012 22:32 — Editoval Aquabellla (13. 04. 2012 22:39)
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Vyšetření množiny bodů
↑ souteh:
Ahoj, u těchto příkladů je strašně důležitý náčrtek.
Příklad 1:
Načrtla jsem kružnici s poloměrem 5 a bod S, kde |SM|=3. Udělala jsem několik ukázkových kružnic, které se dotýkají "hlavní" kružnice a procházejí bodem M. Středy těchto "menších" kružnice jsou označeny G, H, I, J, K, O, P. Je vidět, že body tvoří elipsu s ohnisky v bodech M a S.
"Hlavní" kružnice je kružnicí řídící elipsy (se středem v ohnisku a poloměrem 2a. Platí věta: "Množina všech bodů souměrně sdružených s jedním ohniskem elipsy podle jejích tečen je řídicí kružnice elipsy o středu ve druhém ohnisku a poloměru 2a."
Podrobnosti o elipse si můžeš přečíst například zde.
Příklad 2:
b) Toto je přesně definice paraboly - vzdálenost od ohniska a vzdálenost od řídící přímky je stejná.
a), c) nejsou to paraboly ve smyslu analytické geometrie, ale ve smyslu kvadratické rovnice, která je pootočená o 90° v kartézských souřadnicích.
Příklad 3:
Opět parabola. Náčrtek zde: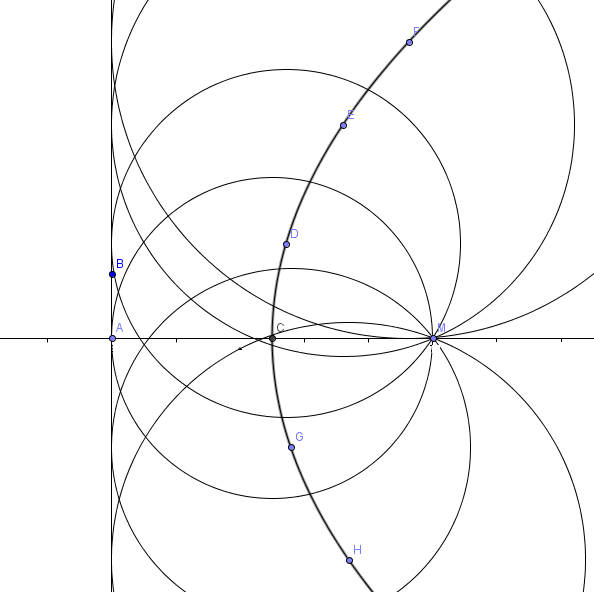
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
