Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita funkce dvou proměnných (TOTO TÉMA JE VYŘEŠENÉ)
#1 14. 04. 2012 18:07
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Limita funkce dvou proměnných
Zdravím, mám limitu dvou proměnných: ![kopírovat do textarea $\lim_{(x,y) \to (1,0)} \frac{\sqrt{x^2 + y^2 - 2x + 2} - 1}{\sqrt[3]{x^2 + y^2 - 2x + 2} - 1}$](/mathtex/1a/1a58b2c65f4ddbbd591fc25cde694386.gif)
Zkusila jsem výraz upravit podle vzorce:  , kde
, kde ![kopírovat do textarea $a = \sqrt[3]{x^2 + y^2 - 2x + 2}$](/mathtex/27/2748213a8d55bc50a5eebcf7e9f22739.gif) a
a  .
.![kopírovat do textarea $\lim_{(x,y) \to (1,0)} \frac{\sqrt{x^2 + y^2 - 2x + 2} - 1}{\sqrt[3]{x^2 + y^2 - 2x + 2} - 1}
\cdot \frac{(x^2 + y^2 - 2x + 2)^{\frac23} + (x^2 + y^2 - 2x + 2)^{\frac13} + 1}{(x^2 + y^2 - 2x + 2)^{\frac23} + (x^2 + y^2 - 2x + 2)^{\frac13} + 1} = \nl
= \lim_{(x,y) \to (1,0)} \frac{(\sqrt{x^2 + y^2 - 2x + 2} - 1) \cdot ((x^2 + y^2 - 2x + 2)^{\frac23} + (x^2 + y^2 - 2x + 2)^{\frac13} + 1)}{x^2 + y^2 - 2x + 2 - 1} = \nl
= \lim_{(x,y) \to (1,0)} \frac{(\sqrt{x^2 + y^2 - 2x + 2} - 1) \cdot ((x^2 + y^2 - 2x + 2)^{\frac23} + (x^2 + y^2 - 2x + 2)^{\frac13} + 1)}{x^2 + y^2 - 2x + 1}$](/mathtex/b5/b582ef0e853a9ba588588e68aaae8732.gif)
A teď nevím, jak pokračovat v úpravě, případně jestli na to jdu správnou cestou. Limita má vyjít  .
.
Předem děkuji za každou pomoc!
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
- (téma jako vyřešené označil(a) Aquabellla)
#2 14. 04. 2012 20:21 — Editoval jarrro (14. 04. 2012 20:25)
Re: Limita funkce dvou proměnných
kvôli kratšiemu zápisu pomôže transformácia  potom
potom![kopírovat do textarea $\frac{\sqrt{3-2\cos{t}}-1}{\sqrt[3]{3-2\cos{t}}-1}=\frac{\left(3-2\cos{t}\right)^{\frac{2}{3}}+\left(3-2\cos{t}\right)^{\frac{1}{3}}+1}{\sqrt{3-2\cos{t}}+1}$](/mathtex/a8/a8519276345216332e8e08dd39e11d9d.gif)
resp. môžeš rovno ešte ten tvoj dlhý zlomok rozšíriť 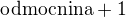 potom
potom
menovateľ sa skráti a dá sa dosadiť je to tuším aj viac košer, lebo transformácia je prakticky len jeden smer čo pri týchto limitách nestačí.
MATH IS THE BEST!!!
Offline
#3 14. 04. 2012 21:51 — Editoval Andrejka3 (14. 04. 2012 21:51)
Re: Limita funkce dvou proměnných
Ahoj, snad nebude vadit, když napíšu svůj návrh. Neříkám, že to je něco nového.
What does a drowning number theorist say?
'log log log log ...'
Offline
#4 15. 04. 2012 14:25
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Limita funkce dvou proměnných
↑ jarrro:
Děkuji, substituce mě nenapadla. Prosím tě, kam jde t, když x jde k jedné a y k nule?
↑ Andrejka3:
Jak ten výraz mám dále upravit? Stále mi to vychází jako nula lomeno nulou, což je neurčitý výraz.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#5 15. 04. 2012 15:07
Re: Limita funkce dvou proměnných
↑ Aquabellla:![kopírovat do textarea $=\lim_{a \to 0^+} \frac{\sqrt{a +1} - 1}{\sqrt[3]{a + 1} - 1}$](/mathtex/e4/e413ec41951e200ab7e9664758fba058.gif)
 .
.
Oznacme 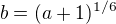 .
.
Pak ![kopírovat do textarea $\frac{\sqrt{a +1} - 1}{\sqrt[3]{a + 1} - 1}=\frac{b^3-1}{b^2-1}=\frac{b^2+b+1}{b+1}$](/mathtex/57/57cb59de1d099698155fbe4499368a79.gif)
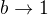 pro
pro 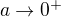 , tedy lim je 3/2.
, tedy lim je 3/2.
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 15. 04. 2012 16:20
- Aquabellla

- Moderátorka Bellla

- Místo: Brno
- Příspěvky: 1473
- Škola: Ma-Ek PřF MUNI (11-14, Bc.), (14-16, Mgr.)
- Pozice: Absolventka Bc., studentka NMgr.
- Reputace: 98
Re: Limita funkce dvou proměnných
↑ Andrejka3:
Děkuji moc.
Nejkratší matematický vtip: „Nechť epsilon je záporné…“
Zákon pro pedagogy: Nikdo vás neposlouchá, dokud se nespletete.
Offline
#7 17. 04. 2012 10:21
Re: Limita funkce dvou proměnných
↑ Aquabellla:t ide k nule,ale to je len jeden smer lepšie je asi nesubstituovať a rovno rozširovať keď substitúcia tak skorej tá od Andrejky tá goniometrická ma napadla ako prvá,ale neviem či je najvhodnejšia
MATH IS THE BEST!!!
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita funkce dvou proměnných (TOTO TÉMA JE VYŘEŠENÉ)

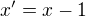 a pak přeznačením
a pak přeznačením 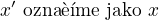
![kopírovat do textarea $\lim_{(x,y) \to (1,0)} \frac{\sqrt{x^2 + y^2 - 2x + 2} - 1}{\sqrt[3]{x^2 + y^2 - 2x + 2} - 1}=\lim_{(x,y) \to (0,0)} \frac{\sqrt{x^2 + y^2 +1} - 1}{\sqrt[3]{x^2 + y^2 + 1} - 1}=$](/mathtex/d7/d7f3681b580711117fdb063ebec4f873.gif)
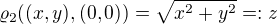 , čímž je vpodstatě problém převeden na limitu v
, čímž je vpodstatě problém převeden na limitu v  :
:![kopírovat do textarea $=\lim_{z \to 0^+} \frac{\sqrt{z^2 +1} - 1}{\sqrt[3]{z^2 + 1} - 1}=$](/mathtex/5b/5b315bb965088d7d104272f76911a904.gif) zřejmě můžeme substituovat (věta o limitě složené fce)
zřejmě můžeme substituovat (věta o limitě složené fce) 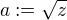 :
:![kopírovat do textarea $=\lim_{a \to 0^+} \frac{\sqrt{a +1} - 1}{\sqrt[3]{a + 1} - 1}$](/mathtex/47/47f13a667051a36429f7bd2a42fd9f52.gif) , což už jde dopočítat.
, což už jde dopočítat.