Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 14. 04. 2012 18:11 — Editoval jahodka007 (14. 04. 2012 18:12)
- jahodka007
- Příspěvky: 49
- Reputace: 0
integrovanie - substitucna metoda
zdravim, neviem pohnut s tymito prikladmi :/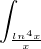 dx
dx  dx
dx![kopírovat do textarea $\int_{x^{2}*\sqrt[3]{6-x^{3}}}^{}$](/mathtex/4a/4aa4e239fc68cca6daa790191bda3927.gif) dx
dx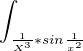 dx
dx
vopred dakujem za rady, pripadne pomoc
ospravedlnujem sa, neviem tu v tyhto vzorcoch pisat- tie cisla maju byt zarovno integralu
Offline
#2 14. 04. 2012 18:18 — Editoval Sam_Hawkins (14. 04. 2012 18:24)
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Re: integrovanie - substitucna metoda
1)
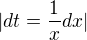
takze dostanes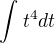
2)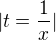
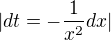
->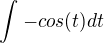
3)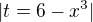

->![kopírovat do textarea $-\frac{1}{3}\int_{}^{}\sqrt[3]{t}dt$](/mathtex/ec/ecc4346b957f30476c297c35cec05214.gif)
4)
tenhle bys uz mel zvladnout sam(a?) odvozenim z predchozich :)
Offline