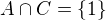Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 04. 2012 14:57 — Editoval constr (25. 04. 2012 19:52)
vlastnosti grup vnitřních automorfismů
Pěkné odpoledne přeji.
Následující 3 úlohy, které jsou těsně spjaty, pocházejí z knihy Group theory I.; Michio Suzuki. Jejich řešení jsem nedokončil.
Definice:
Základní věty (bez důkazů):
1. Nechť
 je grupa taková, že její centrum
je grupa taková, že její centrum 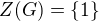 je triviální. Ukažte, že centralizér grupy vnitřních autmorfismů
je triviální. Ukažte, že centralizér grupy vnitřních autmorfismů 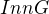 v grupě automorfismů
v grupě automorfismů  je
je 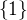 a že
a že 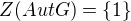 .
.2. Uvažte, že
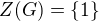 a
a 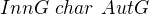 . Nechť
. Nechť 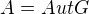 . Ukažte, že každý automorfismus grupy
. Ukažte, že každý automorfismus grupy  je vnitřní.
je vnitřní.Návod:
3. Nechť
 je neabelovská jednoduchá grupa. Ukažte, že libovolný automorfismus z
je neabelovská jednoduchá grupa. Ukažte, že libovolný automorfismus z 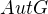 je vnitřní.
je vnitřní. Offline
#2 20. 04. 2012 17:17 — Editoval ruamaixanh (20. 04. 2012 17:47)
- ruamaixanh

- Místo: Tachov
- Příspěvky: 100
- Reputace: 11
Re: vlastnosti grup vnitřních automorfismů
Zdravím,
1) Uvažujme homomorfismus 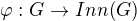 , kde
, kde 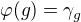 (
( značí konjugace podle
značí konjugace podle  ). Není těžké dokázat, že
). Není těžké dokázat, že 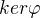 je
je 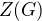 , což je podle zadání
, což je podle zadání  . Homomorfismus je také zřejmě surjektivní, a proto
. Homomorfismus je také zřejmě surjektivní, a proto  . Dále platí:
. Dále platí: 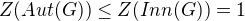 , protože
, protože 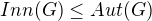
Edit:  ještě neznamená, že
ještě neznamená, že  . Předpokládejme, že
. Předpokládejme, že 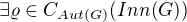 , pak pro každé
, pak pro každé 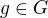 platí:
platí: 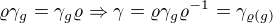 pro každé
pro každé  pro každé
pro každé 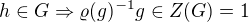 , a proto
, a proto  je identita.
je identita.
Offline
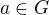 je definovaný jako množina
je definovaný jako množina 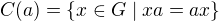
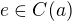 , a proto jestliže
, a proto jestliže 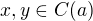 , potom
, potom 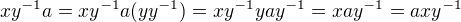 , takže
, takže 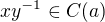 . Proto
. Proto 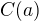 je podgrupa grupy
je podgrupa grupy 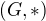 je grupa, potom
je grupa, potom  je
je 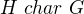 ) jestliže každý automorfismus
) jestliže každý automorfismus 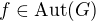 a
a 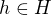 potom
potom 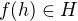
 jsou podgrupy grupy
jsou podgrupy grupy 
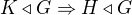
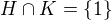
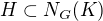
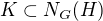
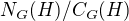 je izomorfní podgrupě
je izomorfní podgrupě 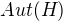 . Protože
. Protože  a
a 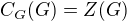 jako důsledek dostáváme, že
jako důsledek dostáváme, že 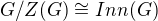 ; tedy, jestliže
; tedy, jestliže  (píše
(píše 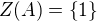 . Můžeme uvažovat že
. Můžeme uvažovat že 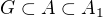 Z věty B1(2) dostáváme že
Z věty B1(2) dostáváme že 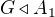 . Konjugace prvkem
. Konjugace prvkem 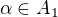 indukuje automorfismus
indukuje automorfismus  v
v  grupy
grupy  a
a 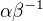 komutují se všemi prvky
komutují se všemi prvky 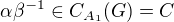 . Dokažte
. Dokažte 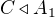 a
a