Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 04. 2012 13:46
Posloupnosti
Zdravím,
mám tu příklad z Petákové s kterým se mi nedaří hnout.
Součet tří po sobě jdoucích členů geometrické posloupnosti je 9. První číslo necháme, druhé číslo zvětšíme o 12 a třetí číslo zmenšíme o 3. Dostaneme tak tři po sobě jdoucí členy aritmetické posloupnosti. Určete původní trojici čísel a proveďte zkoušku.
Trochu naznačím kam jsem došel..
členy jsem si označil x;y;z
Platí pro ně, že součet GP těchto členů je roven 9.
dále z věty o AP mohu zjistit, že součet 3 členů AP je
Z toho vím teda, že
a dále vím, že pro GP platí
Kvocient se pokusím vyjádřit aby obsahoval x a z, takže pokud se nepletu

proto
Což když dosadím do 
Tak se mi nedaří vypočítat...
Nešlo by to nějak jednodušeji?:)
Díky!
Baf!
Offline
- (téma jako vyřešené označil(a) elypsa)
#2 22. 04. 2012 15:14
Re: Posloupnosti
↑ elypsa:
Zdravím...
Označíme se dané tři členy 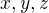 .
.
Pak 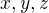 tvoří geometrickou posloupnost, a členy
tvoří geometrickou posloupnost, a členy  aritmetickou posloupnost.
aritmetickou posloupnost.
Platí: 
 (plyne z toho, x,y,z tvoří GP, kvocient musí být stejný pro podíl sousedních členů))
(plyne z toho, x,y,z tvoří GP, kvocient musí být stejný pro podíl sousedních členů))
 (plyne z toho, že dané členy tvoří AP - diference sousedních členů musí být stejná).
(plyne z toho, že dané členy tvoří AP - diference sousedních členů musí být stejná).
Dostali jsme tedy soustavu tří rovnic o 3 neznámých.
Např. z 1. a 3. rovnice vypočítáme  , zbylé dvě neznámé dopočtem...
, zbylé dvě neznámé dopočtem...
Výsledkem jsou 2 řešení:  a
a  .
.
Offline

 (1)
(1)


 , dosadíš
, dosadíš
 dosadíš z (1)
dosadíš z (1)

 a je to
a je to a má být 12
a má být 12