Matematické Fórum

petia · 03. 03. 2012 18:47

Určete výšku hory, vidíme-li její vrchol ze stanoviště 15m nad hladinou vody ve výškovém úhlu alfa=28°37‘ a obraz vrcholu ve vodě pod hloubkovým úhlem beta=42°20‘.

Andrejka3 · 05. 03. 2012 08:23

Ahoj. Je to jeste aktualni? Mohla bych vecer odpovedet. Napis kdyztak.
A

petia · 05. 03. 2012 15:30

Zdravím, jjj. Je to aktuální. Má mi vyjít 23.9835m

Rumburak · 05. 03. 2012 16:16

↑ petia:
Nakresli si obrázek. K sestavení rovnic budeš potřebovat ještě poznatek z optiky, že při odrazu paprsku od lesklé plochy je úhel odrazu roven úhlu dopadu.

petia · 05. 03. 2012 17:01

Kde je chyba?
http://forum.matweb.cz/upload3/img/2012 … 2Bhory.jpg

Andrejka3 · 05. 03. 2012 20:32

Ahoj. Číselné dosazení jsem nekontrolovala, ale postup se mi zdá vpořádku.

petia · 05. 03. 2012 21:01

Ahojky. Právě tam musím mít někde chybu. Má mi vyjít 23,9835m. A mě vyšlo skoro 60.
Nemůžu přijít na to, kde tu chybu mám.

Andrejka3 · 05. 03. 2012 21:26

Vyslo mi totez.

mák · 05. 03. 2012 22:17

Aktuální výška "hloubkového úhlu" v závislosti na vodorovné vzdálenosti x: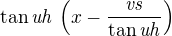
$\tan {\it uh}\,\left(x-{{{\it vs}}\over{\tan {\it uh}}}\right)$
Aktuální výška "výškového úhlu" v závislosti na vodorovné vzdálenosti x:
$\tan {\it uv}\,x+{\it vs}$
Hledáme místo kde se úhly zkříží - sestavená rovnice:
$\tan {\it uh}\,\left(x-{{{\it vs}}\over{\tan {\it uh}}}\right)= \tan {\it uv}\,x+{\it vs}$
Kde:
uh - hloubkový úhel
uv - výškový úhel
vs - výška stanoviště
x - vodorovná vzdálenost hory od stanoviště

Pak x se rovná:
$x=-{{2\,{\it vs}}\over{\tan {\it uv}-\tan {\it uh}}}$

A dosazením do levé nebo pravé strany rovnice vyjde výška:
$vyska = \left(1-{{2\,\tan {\it uv}}\over{\tan {\it uv}-\tan {\it uh}}} \right)\,{\it vs}$

${\it vyska}=59.7944788176905$
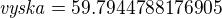
No a vyšlo mi ta taky stejně.